WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

GaborFilter
✖
GaborFilter

✖
GaborFilter[data,r,k]

filters data by convolving with a Gabor kernel of pixel radius r and wave vector k.

✖
GaborFilter[data,r,k,ϕ]

uses a Gabor kernel with phase shift ϕ.

✖
GaborFilter[data,{r,σ},…]

uses a Gabor kernel with radius r and standard deviation σ.

Details and Options

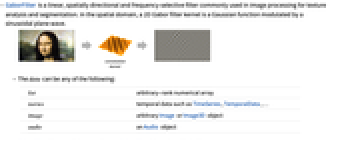
  • GaborFilter is a linear, spatially directional and frequency-selective filter commonly used in image processing for texture analysis and segmentation. In the spatial domain, a 2D Gabor filter kernel is a Gaussian function modulated by a sinusoidal plane wave.
  • The data can be any of the following:
  • listarbitrary-rank numerical array
    tseriestemporal data such as TimeSeries, TemporalData, …
    imagearbitrary Image or Image3D object
    audioan Audio object
  • GaborFilter[data,r,k] is equivalent to GaborFilter[data,{r,r/2},k,0].
  • Either of the r or σ can be lists, specifying different values for different directions.
  • GaborFilter[image,…] by default gives an image of a real type of the same dimensions as image.
  • The following options can be specified:
  • Padding "Fixed"padding method
    StandardizedTruewhether to rescale the Gabor kernel to account for truncation
    WorkingPrecision Automaticthe precision to use
  • With a setting Padding->None, GaborFilter[data,…] normally gives a result smaller than data.

Examples

open allclose all

Basic Examples  (3)Summary of the most common use cases

Filter an image:

In[287]:=287
✖
https://wolfram.com/xid/0fq71z0ltch0a-fjpioi
Out[287]=287

Gabor filtering of a 3D image:

In[1]:=1
✖
https://wolfram.com/xid/0fq71z0ltch0a-dcmdxe
Out[1]=1

Apply a Gabor filter to a list of values:

In[1]:=1
✖
https://wolfram.com/xid/0fq71z0ltch0a-dvgi9o
Out[1]=1

Scope  (7)Survey of the scope of standard use cases

Data  (4)

Gabor filtering of a 2D array:

In[154]:=154
✖
https://wolfram.com/xid/0fq71z0ltch0a-ddmrxe
Out[156]=156

Filter a TimeSeries object:

In[1]:=1
✖
https://wolfram.com/xid/0fq71z0ltch0a-j6ug3v
In[2]:=2
✖
https://wolfram.com/xid/0fq71z0ltch0a-frwn5n
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0fq71z0ltch0a-iwyhx
Out[3]=3

Filter an Audio signal:

In[1]:=1
✖
https://wolfram.com/xid/0fq71z0ltch0a-emvukp
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0fq71z0ltch0a-iqqsr
Out[2]=2

Filter a color image:

In[1]:=1
✖
https://wolfram.com/xid/0fq71z0ltch0a-evjhyd
Out[1]=1

Parameters  (3)

Gabor filtering of a noisy signal using different kernel radii:

In[72]:=72
✖
https://wolfram.com/xid/0fq71z0ltch0a-ekel2p
In[10]:=10
✖
https://wolfram.com/xid/0fq71z0ltch0a-c7x15i
Out[11]=11

Use different standard deviations:

In[20]:=20
✖
https://wolfram.com/xid/0fq71z0ltch0a-kgyzk0
Out[21]=21

Use different wave vectors:

In[75]:=75
✖
https://wolfram.com/xid/0fq71z0ltch0a-j7z1m
Out[76]=76

Gabor filtering in the vertical direction:

In[1]:=1
✖
https://wolfram.com/xid/0fq71z0ltch0a-hekrt
Out[1]=1

Filtering in the horizontal direction:

In[2]:=2
✖
https://wolfram.com/xid/0fq71z0ltch0a-cwon47
Out[2]=2

Filtering in a diagonal direction:

In[3]:=3
✖
https://wolfram.com/xid/0fq71z0ltch0a-e0sxr6
Out[3]=3

The cosine part of a Gabor filter is computed when :

In[1]:=1
✖
https://wolfram.com/xid/0fq71z0ltch0a-y35oh
Out[1]=1

The sine part of a Gabor filter is computed when :

In[2]:=2
✖
https://wolfram.com/xid/0fq71z0ltch0a-cioi27
Out[2]=2

Options  (6)Common values & functionality for each option

Padding  (3)

Gabor filtering using different padding schemes:

In[1]:=1
✖
https://wolfram.com/xid/0fq71z0ltch0a-j2ihmz
In[3]:=3
✖
https://wolfram.com/xid/0fq71z0ltch0a-ggz55e
Out[3]=3

Gabor filtering of a grayscale image using different padding schemes:

In[1]:=1
✖
https://wolfram.com/xid/0fq71z0ltch0a-brspfd
Out[1]=1

Padding->None normally returns an image smaller than the input image:

In[1]:=1
✖
https://wolfram.com/xid/0fq71z0ltch0a-bkzy48
Out[1]=1

WorkingPrecision  (3)

MachinePrecision is by default used with integer arrays:

In[1]:=1
✖
https://wolfram.com/xid/0fq71z0ltch0a-cdrg18
Out[1]=1

Perform exact computation instead:

In[2]:=2
✖
https://wolfram.com/xid/0fq71z0ltch0a-jt3a9c
Out[2]=2

With real arrays, by default the precision of the input is used:

In[1]:=1
✖
https://wolfram.com/xid/0fq71z0ltch0a-2q79si
Out[1]=1

Specify the precision to use:

In[2]:=2
✖
https://wolfram.com/xid/0fq71z0ltch0a-7f69wx
Out[2]=2

WorkingPrecision is ignored when filtering images:

In[1]:=1
✖
https://wolfram.com/xid/0fq71z0ltch0a-pc6p9y
Out[1]=1

An image of a real type is always returned:

In[2]:=2
✖
https://wolfram.com/xid/0fq71z0ltch0a-o6dztt
Out[2]=2

Applications  (3)Sample problems that can be solved with this function

Gabor filtering of an image to detect vertical lines in an image:

In[106]:=106
✖
https://wolfram.com/xid/0fq71z0ltch0a-yayl71
Out[106]=106

Detect edges in the specified direction in a noisy image:

In[1]:=1
✖
https://wolfram.com/xid/0fq71z0ltch0a-dkjmn3
Out[1]=1

The magnitude of the Gabor filter is computed as the squared norm of the sine and cosine components:

In[1]:=1
✖
https://wolfram.com/xid/0fq71z0ltch0a-fqopmr

Extract regions with the dominant direction parallel to and :

In[2]:=2
✖
https://wolfram.com/xid/0fq71z0ltch0a-vjwmcr
Out[2]=2

Highlight two texture segments on the image:

In[3]:=3
✖
https://wolfram.com/xid/0fq71z0ltch0a-fzo2nr
Out[3]=3

Properties & Relations  (5)Properties of the function, and connections to other functions

GaborFilter is equivalent to a convolution with a GaborMatrix:

In[13]:=13
✖
https://wolfram.com/xid/0fq71z0ltch0a-es6t43
Out[14]=14
In[15]:=15
✖
https://wolfram.com/xid/0fq71z0ltch0a-ri8l57
Out[15]=15
In[16]:=16
✖
https://wolfram.com/xid/0fq71z0ltch0a-bfgtky
Out[16]=16

Gabor filtering with a zero-valued wave vector is equivalent to Gaussian smoothing:

In[1]:=1
✖
https://wolfram.com/xid/0fq71z0ltch0a-cw7vc0
Out[1]=1

Impulse response of a Gabor filter:

In[1]:=1
✖
https://wolfram.com/xid/0fq71z0ltch0a-byrh8v
Out[1]=1

Magnitude spectrum of the filter:

In[2]:=2
✖
https://wolfram.com/xid/0fq71z0ltch0a-fpgj9e
Out[2]=2

Gabor filtering of an image gives a real-valued image:

In[1]:=1
✖
https://wolfram.com/xid/0fq71z0ltch0a-hznxi1
Out[1]=1

GaborFilter is a linear filter:

In[1]:=1
✖
https://wolfram.com/xid/0fq71z0ltch0a-dktmv8
Out[1]=1
Wolfram Research (2012), GaborFilter, Wolfram Language function, https://reference.wolfram.com/language/ref/GaborFilter.html (updated 2016).
✖
Wolfram Research (2012), GaborFilter, Wolfram Language function, https://reference.wolfram.com/language/ref/GaborFilter.html (updated 2016).

Text

Wolfram Research (2012), GaborFilter, Wolfram Language function, https://reference.wolfram.com/language/ref/GaborFilter.html (updated 2016).

✖
Wolfram Research (2012), GaborFilter, Wolfram Language function, https://reference.wolfram.com/language/ref/GaborFilter.html (updated 2016).

CMS

Wolfram Language. 2012. "GaborFilter." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/GaborFilter.html.

✖
Wolfram Language. 2012. "GaborFilter." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/GaborFilter.html.

APA

Wolfram Language. (2012). GaborFilter. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GaborFilter.html

✖
Wolfram Language. (2012). GaborFilter. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GaborFilter.html

BibTeX

@misc{reference.wolfram_2025_gaborfilter, author="Wolfram Research", title="{GaborFilter}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/GaborFilter.html}", note=[Accessed: 01-April-2025 ]}

✖
@misc{reference.wolfram_2025_gaborfilter, author="Wolfram Research", title="{GaborFilter}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/GaborFilter.html}", note=[Accessed: 01-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_gaborfilter, organization={Wolfram Research}, title={GaborFilter}, year={2016}, url={https://reference.wolfram.com/language/ref/GaborFilter.html}, note=[Accessed: 01-April-2025 ]}

✖
@online{reference.wolfram_2025_gaborfilter, organization={Wolfram Research}, title={GaborFilter}, year={2016}, url={https://reference.wolfram.com/language/ref/GaborFilter.html}, note=[Accessed: 01-April-2025 ]}