HardcorePointProcess
HardcorePointProcess[μ,rh,d]
表示 ![]() 中的硬核点过程,具有恒定强度 μ,硬核半径为 rh.
中的硬核点过程,具有恒定强度 μ,硬核半径为 rh.
更多信息


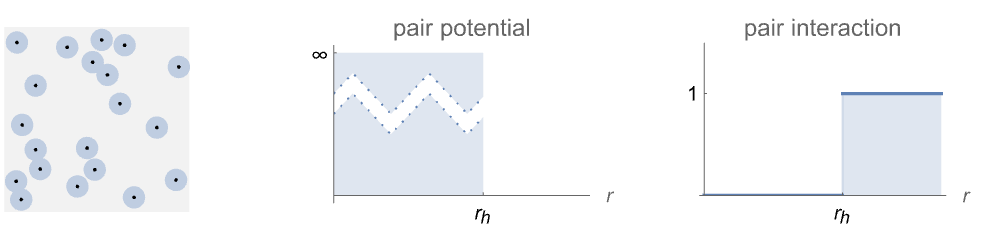
- HardcorePointProcess 模拟一种点布局,其中的点不能位于彼此的半径 rh 之内,除此之外,则呈均匀分布,每单位体积内的强度为 μ 个点.
- 当点的行为类似于一组玻璃弹子时,通常使用硬核模型,包括气体分子、金属沉积物、烧结材料和生物细胞等.
-
- 硬核点过程可用强度为 μ、对势为
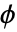 或偶相互酌为
或偶相互酌为 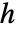 的 GibbsPointProcess 来定义,可用 rh 来参数化两个函数:
的 GibbsPointProcess 来定义,可用 rh 来参数化两个函数: -
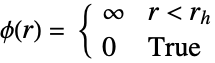
对势 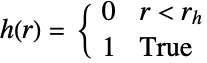
偶相互酌 - 观察区域 reg 中的硬核点过程 HardcorePointProcess[μ,rh,d] 的点布局
 的密度函数
的密度函数 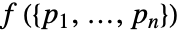 相对于 PoissonPointProcess[1,d],与
相对于 PoissonPointProcess[1,d],与 ![mu^n product_(i!=j)Boole[||p_i-p_j||>r_(h)] mu^n product_(i!=j)Boole[||p_i-p_j||>r_(h)]](Files/HardcorePointProcess.zh/9.png) 成正比.
成正比. - 将点
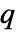 添加到点布局
添加到点布局  中的 Papangelou 条件密度
中的 Papangelou 条件密度 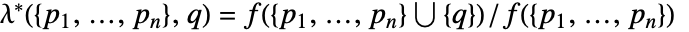 为
为 ![mu product_iBoole[||p_i-q||>r_(h)] mu product_iBoole[||p_i-q||>r_(h)]](Files/HardcorePointProcess.zh/13.png) .
. - HardcorePointProcess 允许 μ 和 rh 为任意正数,允许 d 为任意正整数.
- HardcorePointProcess 是 GibbsPointProcess 的特例,相当于 StraussPointProcess[μ, 0, rh].
- RandomPointConfiguration 中针对 HardcorePointProcess 的可能的 Method 设置为:
-
"MCMC" MCMC 生灭法 "Exact" 从过去出发的耦合 - HardcorePointProcess 的 EstimatedPointProcess 中可能的 PointProcessEstimator 的设置为:
-
Automatic 自动选择参数估计器 "MaximumPseudoLikelihood" 最大化伪似然性 - HardcorePointProcess 可与诸如 RipleyK 和 RandomPointConfiguration 这样的函数一起使用.
范例
打开所有单元关闭所有单元范围 (3)
选项 (4)
属性和关系 (3)
Wolfram Research (2020),HardcorePointProcess,Wolfram 语言函数,https://reference.wolfram.com/language/ref/HardcorePointProcess.html.
文本
Wolfram Research (2020),HardcorePointProcess,Wolfram 语言函数,https://reference.wolfram.com/language/ref/HardcorePointProcess.html.
CMS
Wolfram 语言. 2020. "HardcorePointProcess." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/HardcorePointProcess.html.
APA
Wolfram 语言. (2020). HardcorePointProcess. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/HardcorePointProcess.html 年