HermitianMatrixQ

HermitianMatrixQ[m]

m が明示的にエルミート(Hermite)行列の場合はTrueを，その他の場合はFalseを返す．

詳細とオプション

  • HermitianMatrixQは自己随伴行列としても知られている．
  • m==ConjugateTranspose[m]のとき，行列 m はエルミート行列である．
  • HermitianMatrixQは数値行列と記号行列の両方に使うことができる．
  • 使用可能なオプション
  • SameTest Automatic式の等価性を検定する関数
    Tolerance Automatic近似数の許容範囲
  • 厳密行列および記号行列については，オプションSameTest->f は，f[mij,mkl]がTrueを返す場合は mijおよび mklの2項が等価であると考えられることを示す．
  • 近似行列については，オプションTolerance->t を使ってAbs[mij]≤t であるすべての項がゼロであると考えられることを示す．
  • Abs[mij]>t である行列の項については，等価性の比較は最後の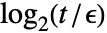ビットを除いて行われる．ただし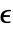， はMachinePrecision行列については$MachineEpsilon，Precision 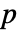の行列については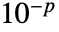である．

例題

すべて開くすべて閉じる

例  (2)

2×2数値行列が明示的なエルミート行列かどうかの検定を行う：

3×3記号行列が明示的なエルミート行列かどうかの検定を行う：

スコープ  (10)

基本的な用法  (6)

機械精度の実行列がエルミート行列かどうかの検定を行う：

実エルミート行列は対称行列でもある：

複素行列がエルミート行列かどうかの検定を行う：

複素エルミート行列には対称な実部と非対称な虚部がある：

厳密行列がエルミート行列かどうかの検定を行う：

行列をエルミート行列にする：

HermitianMatrixQを任意精度行列に使う：

ランダム行列は，通常は，エルミート行列ではない：

HermitianMatrixQを記号行列に使う：

c=TemplateBox[{b}, Conjugate]で対角成分が明示的に実数値のとき，行列はエルミート行列になる：

HermitianMatrixQは大きい数値行列に効率的に機能する：

特殊行列  (4)

HermitianMatrixQをそな行列に使う：

HermitianMatrixQを構造化行列に使う：

QuantityArrayを構造化行列に使う：

恒等行列はエルミート行列である：

HilbertMatrixはエルミート行列である：

オプション  (2)

SameTest  (1)

この行列は正の実数 についてはエルミート行列であるが，HermitianMatrixQはFalseを返す：

オプションSameTestを使って正しい答を得る：

Tolerance  (1)

次数10-14のランダムな摂動のある複素数値エルミート行列を生成する：

この行列をエルミート行列として許容するように，オプションToleranceを調節する：

この行列とその共役転置行列の差のノルム：

アプリケーション  (8)

エルミート行列の起源  (5)

エルミート関数 によって生成された行列はエルミート行列である：

この関数はエルミート関数である：

Tableを使うとエルミート行列が生成される：

SymmetrizedArrayは対称性を持つ行列（および一般配列）が生成できる：

Normalを使って一般行列に変換し直す：

Pauli行列はエルミート行列である：

複素データの統計尺度の中にはCovarianceを含むエルミート行列がある：

Correlation：

AbsoluteCorrelation：

GaussianUnitaryMatrixDistributionから導かれた行列はエルミート行列である：

GaussianSymplecticMatrixDistributionから導かれた行列はエルミート行列である：

エルミート行列の用法  (3)

正定値エルミート行列つまり測定基準 は によって内積を定義する：

が，実際に，エルミート行列で正定値であることを確認する：

TemplateBox[{}, Complexes]^nの標準基底を直交化することで正規直交基底を求める：

この基底が内積について正規直交であることを確認する：

量子力学では，時間発展はユニタリ行列 の1パラメータ族で表される． 掛ける の対数微分はハミルトニアンあるいはエネルギー演算子 と呼ばれるエルミート行列で，その固有値は系の可能なエネルギーを表す．次の時間発展についてハミルトニアンと可能なエネルギーを計算する：

まず， と が実数であるという仮定の下で行列が実際にユニタリ行列であることを確認する：

対数微分を計算する：

この行列は反エルミート行列である：

ハミルトニアンを定義する：

この行列がエルミート行列であることを確認する：

その実固有値は可能なエネルギーを表す：

一般的なメソッドへのフェイルオーバーがある別の方法を，エルミート行列に使う：

検定のために複素行列を構築する：

非エルミート行列mについては，myLSはガウス消去法のみを使う：

不定値エルミート行列mhについては，コレスキー(Cholesky)法を試み，続けてガウス消去法を用いる：

正定値エルミート行列mpdについては，コレスキー法を試みる，これは成功する：

特性と関係  (16)

HermitianMatrixQ[x]は行列ではない任意の x についてFalseを自明に返す：

m==ConjugateTranspose[m]のとき，その行列はエルミート行列である：

エルミート行列には実数の対角要素がなければならない：

Diagonalを使って対角要素を取り出す：

実数値対称行列はエルミート行列である：

しかし，複素対称行列は，そうではない可能性がある：

Symmetrizeを対称Hermitianに使って行列のエルミート部分を計算する：

これは m とConjugateTranspose[m]の平均に等しい：

任意の行列を，エルミート部分と反エルミート部分の和で表すことができる：

AntihermitianMatrixQを使って行列が反エルミート行列かどうかを確かめる：

がエルミート行列なら は反エルミート行列である：

MatrixExp[I h]は任意のエルミート行列 h についてユニタリである：

エルミート行列は常に正規行列である：

NormalMatrixQを使って行列が正規行列かどうか確かめる：

エルミート行列の固有値はすべて実数である：

Eigenvaluesを使って固有値を求める：

エルミート行列 m についてのCharacteristicPolynomial[m,x]は実係数を持つ：

さらに，線形項に因子分解できる：

エルミート行列は，固有ベクトルの完全集合を持つ：

結果として，それらは対角化可能でなければならない：

Eigenvectorsを使って固有ベクトルを求める：

エルミート行列は実数値の行列式を持つ：

Detを使って行列式を計算する：

エルミート行列の逆行列はエルミート行列である：

MatrixExpを含むエルミート行列の実数値行列関数はエルミート行列である：

任意の一変量解析関数はMatrixFunctionを使って表現することができる：

行列の整数乗はハミルトン行列であるが非整数乗はそうではない点に注意のこと：

HermitianMatrixを使ってエルミート行列を明示的に構築することができる：

これはHermitianMatrixQを満足する：

考えられる問題  (1)

複素対称行列はエルミート行列ではない：

Wolfram Research (2007), HermitianMatrixQ, Wolfram言語関数， https://reference.wolfram.com/language/ref/HermitianMatrixQ.html （2014年に更新）.

テキスト

Wolfram Research (2007), HermitianMatrixQ, Wolfram言語関数， https://reference.wolfram.com/language/ref/HermitianMatrixQ.html （2014年に更新）.

CMS

Wolfram Language. 2007. "HermitianMatrixQ." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/HermitianMatrixQ.html.

APA

Wolfram Language. (2007). HermitianMatrixQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HermitianMatrixQ.html

BibTeX

@misc{reference.wolfram_2024_hermitianmatrixq, author="Wolfram Research", title="{HermitianMatrixQ}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/HermitianMatrixQ.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_hermitianmatrixq, organization={Wolfram Research}, title={HermitianMatrixQ}, year={2014}, url={https://reference.wolfram.com/language/ref/HermitianMatrixQ.html}, note=[Accessed: 22-November-2024 ]}