HoytDistribution

HoytDistribution[q,ω]

形状母数 q，拡散母数 ω のHoyt分布を表す．

詳細

  • HoytDistributionは仲上- 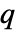分布としても知られている．
  • 値 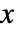の確率密度は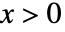，では x exp(-((1+q^2)^2 x^2)/(4 q^2 omega)) TemplateBox[{0, {{(, {{(, {1, -, {q, ^, 4}}, )}, , {x, ^, 2}}, )}, /, {(, {4, , {q, ^, 2}, , omega}, )}}}, BesselI]に比例し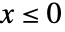，では0である．
  • HoytDistributionでは，q は0から1までの任意の数でよく，ω は任意の正の実数でよい．
  • HoytDistributionでは，ω は任意の単位次元の数量でよく，q は無次元量でよい． »
  • HoytDistributionは，Mean，CDF，RandomVariate等の関数とともに用いることができる．

予備知識

  • HoytDistribution[q,ω]は，区間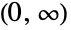上で定義された連続統計分布を表す．この分布は正の実数 q (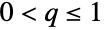)および ω によってパラメータ化される．両者はそれぞれ「形状母数」および「拡散母数」と呼ばれるものである．Hoyt分布の確率密度関数(PDF)は単峰性で，母数 q および ω が，PDFの全体的な高さ，傾き，凹面を決定する．加えて，Hoyt分布のPDFの裾部は，PDF
    が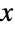 の大きい値について指数的に減少するという意味で「薄い」（この動作は，分布のSurvivalFunctionを分析することで，数量的に正確にすることができる）．Hoyt分布は仲上 q 分布あるいは仲上・Hoyt分布として参照されることがあるが，これをNakagamiDistributionと混同してはならない．
  • Hoyt分布は，1940年代にR. S. Hoytによって，また1960年代に仲上稔によって，別々に研究された．Hoytによるものは，より理論的で複素変量に関連する確率関数に焦点を当てたものであるのに対し，仲上によるものは，極端なフェージングにおける電波強度のモデリングを助けるために考案された分布である．仲上の業績以来，Hoyt分布の応用は，フェージングが存在する中での無線セルラーや電波信号の伝播のモデリングにも応用されている．
  • RandomVariateを使って，Hoyt分布から，1つあるいは複数の機械精度あるいは任意精度（後者はWorkingPrecisionオプションを介す）の擬似乱数変量を得ることができる．Distributed[x,HoytDistribution[q,ω]]（より簡略すると xHoytDistribution[q,ω]）を使って，確率変数 x が，Hoyt分布に従って分布していると宣言することができる．このような宣言は，Probability，NProbability，Expectation，NExpectation等の関数で使うことができる．
  • 確率密度関数および累積分布関数は，PDF[HoytDistribution[q,ω],x]およびCDF[HoytDistribution[q,ω],x]を使って得られることがある．平均，中央値，分散，原点の周りのモーメント，中心モーメントは，それぞれMean，Median，Variance，Moment，CentralMomentを使って計算することができる．
  • DistributionFitTestを使って，与えられたデータ集合がHoyt分布と一致するかどうかを検定することが，EstimatedDistributionを使って与えられたデータからパラメトリックHoyt分布を推定することが，FindDistributionParametersを使ってデータをHoyt分布にフィットすることができる．ProbabilityPlotを使って記号Hoyt分布のCDFに対する与えられたデータのCDFのプロットを生成することが，QuantilePlotを使って記号Hoyt分布の変位値に対する与えられたデータの変位値のプロットを生成することができる．
  • TransformedDistributionを使って変換されたHoyt分布を表すことが，CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが，TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる．CopulaDistributionを使ってHoyt分布を含む高次元分布を構築することが，ProductDistributionを使ってHoyt分布を含む独立成分分布の結合分布を計算することができる．
  • HoytDistributionは他の数多くの分布と密接に関係している．例えば，Hoytは，複素変量によってHoytDistributionとNormalDistributionの関係を確立した．さらに，HoytDistributionは，YGammaDistribution[m,ω/m]およびZChiDistribution[2 m]ならば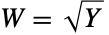，および 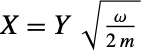がW,XHoytDistribution[m,ω]を満たすという意味で，GammaDistributionとChiDistributionの両方と結びついている．HoytDistributionは，HoytDistribution[q,ω]のPDFが厳密に，q が0に近付く場合のHalfNormalDistribution[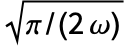]および q が1に近付く場合のRayleighDistribution[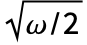]のそれであるという意味で，HalfNormalDistributionおよびRayleighDistributionに近い．HoytDistributionは，NakagamiDistribution，ExponentialDistribution，ArcSinDistribution，BinormalDistribution，BeckmannDistributionとも関連がある．

例題

すべて開くすべて閉じる

例  (3)

確率密度関数：

累積分布関数：

平均と分散：

スコープ  (8)

Hoyt分布から擬似乱数のサンプルを生成する：

そのヒストグラムをその確率密度関数と比較する：

分布母数推定：

サンプルデータから分布母数を推定する：

サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する：

歪度は第1母数のみに依存する：

極限値：

尖度は第1母数のみに依存する：

極限値：

母数の関数としての閉形式の種々のモーメント：

Moment：

記号次数の閉形式：

CentralMoment：

FactorialMoment：

Cumulant：

ハザード関数：

分位関数：

母数でQuantityを一貫して使うとQuantityDistributionが与えられる：

長さの中央値を求める：

アプリケーション  (1)

フェージングチャネル理論では，電離層による強力なシンチレーションが存在する場合に，衛星中継でフェージングする振幅をモデル化するのにHoytDistributionが使用される．， は信号あたりのエネルギー， はホワイトノイズのスペクトル密度として瞬間的な信号対ノイズ比の分布を求める：

モーメント母関数(MGF)を求める：

平均を求める：

モーメント母関数を平均の式で表す：

フェージングの量を求める：

特性と関係  (8)

Hoyt分布族は正の因子によるスケーリングの下では閉じている：

他の分布との関係：

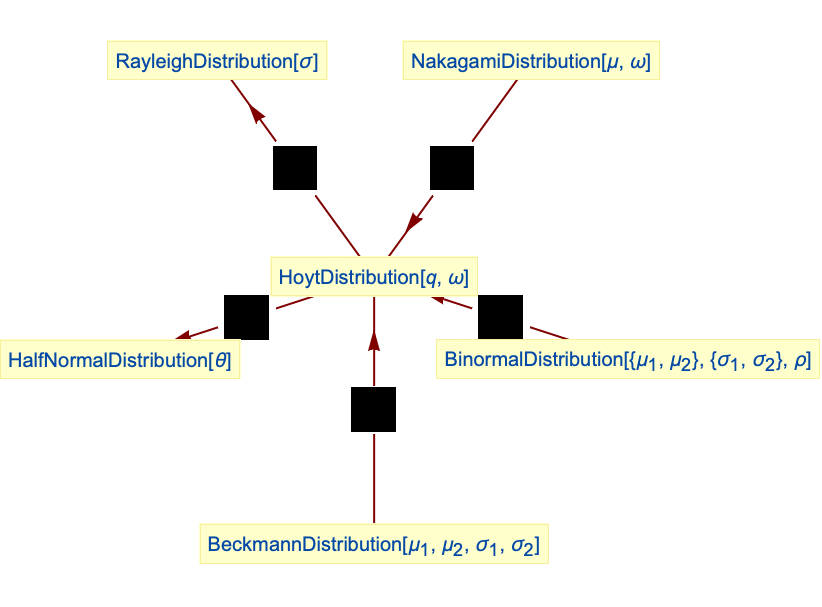
HoytDistributionは のとき，HalfNormalDistributionに簡約される：

のとき，HoytDistributionはRayleighDistribution[Sqrt[ω/2]]に簡約される：

NakagamiDistributionはHoyt分布に関連している：

Hoyt分布はExponentialDistributionとArcSinDistributionから得ることができる：

Hoyt分布はBinormalDistributionから得ることができる：

Hoyt分布はBeckmannDistributionの特殊ケースである：

おもしろい例題  (1)

累積分布関数の等高線を持つ q のさまざまな値についての確率密度関数：

Wolfram Research (2010), HoytDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/HoytDistribution.html （2016年に更新）.

テキスト

Wolfram Research (2010), HoytDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/HoytDistribution.html （2016年に更新）.

CMS

Wolfram Language. 2010. "HoytDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/HoytDistribution.html.

APA

Wolfram Language. (2010). HoytDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HoytDistribution.html

BibTeX

@misc{reference.wolfram_2024_hoytdistribution, author="Wolfram Research", title="{HoytDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/HoytDistribution.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_hoytdistribution, organization={Wolfram Research}, title={HoytDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/HoytDistribution.html}, note=[Accessed: 18-November-2024 ]}