Hyperfactorial

Hyperfactorial[n]

超階乗関数 TemplateBox[{n}, Hyperfactorial]を返す．

詳細

  • 記号操作・数値操作の両方に適した数学関数である．
  • 超階乗関数は，正の整数に 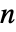ついては TemplateBox[{n}, Hyperfactorial]=product_(k=1)^nk^k，その他の場合は TemplateBox[{z}, Hyperfactorial]=(z/(sqrt(2 pi)))^z exp(1/2 z (z-1)+TemplateBox[{{-, 2}, z}, PolyGamma2])と定義される．
  • 超階乗関数は TemplateBox[{z}, Hyperfactorial]=z^z TemplateBox[{{z, -, 1}}, Hyperfactorial]を満足する．
  • Hyperfactorialは任意の数値精度で評価できる．
  • Hyperfactorialは自動的にリストに縫い込まれる．

例題

すべて開くすべて閉じる

例  (5)

数値的に評価する：

実数の部分集合上でプロットする：

複素数の部分集合上でプロットする：

原点における級数展開：

Infinityにおける級数展開：

スコープ  (28)

数値評価  (6)

数値的に評価する：

高精度で評価する：

出力精度は入力精度に従う：

複素数入力：

高精度で効率的に評価する：

Aroundを使って平均的な場合の統計区間を計算する：

配列の要素ごとの値を計算する：

MatrixFunctionを使って行列のHyperfactorial関数を計算することもできる：

特定の値  (4)

固定点における値：

ゼロにおける値：

Hyperfactorialは，1/2と1/4の整数倍について厳密値を与える：

正の最小値を求める：

可視化  (2)

Hyperfactorial関数をプロットする：

TemplateBox[{z}, Hyperfactorial]の実部をプロットする：

TemplateBox[{z}, Hyperfactorial]の虚部をプロットする：

関数の特性  (11)

Hyperfactorialの実領域：

複素領域：

定義域の連続部分におけるHyperfactorialの値域：

Hyperfactorialは要素単位でリストに縫い込まれる：

Hyperfactorialは解析関数ではない：

有理型でもない：

Hyperfactorialは非増加でも非減少でもない：

Hyperfactorialは単射ではない：

Hyperfactorialは全射ではない：

Hyperfactorialは非負でも非正でもない：

Hyperfactorialは x≤-1のとき特異点と不連続点の両方を持つ：

Hyperfactorialは凸でも凹でもない：

TraditionalFormによる表示：

微分  (2)

n についての一次導関数：

n についての高次導関数：

n についての高次導関数をプロットする：

級数展開  (3)

Seriesを使ってテイラー(Taylor)展開を求める：

の周りの最初の3つの近似をプロットする：

生成点におけるテイラー展開：

Infinityにおける級数展開を求める：

アプリケーション  (3)

Hyperfactorial関数およびExp関数の極限からGlaisherを得る：

エルミート(Hermite)多項式の判別式は超階乗によって表現される：

いくつかの小さい次数についてのファレイ数列のすべての非零要素の積：

閉じた形の式と比較する：

特性と関係  (3)

FullSimplifyとFunctionExpandを使ってHyperfactorialを含む式を簡約する：

HyperfactorialはProductで生成される：

FindSequenceFunctionはHyperfactorial数列を認識する：

おもしろい例題  (2)

二項係数から構築された行列の行列式：

Bernstein多項式から構築された行列の行列式：

Wolfram Research (2008), Hyperfactorial, Wolfram言語関数， https://reference.wolfram.com/language/ref/Hyperfactorial.html.

テキスト

Wolfram Research (2008), Hyperfactorial, Wolfram言語関数， https://reference.wolfram.com/language/ref/Hyperfactorial.html.

CMS

Wolfram Language. 2008. "Hyperfactorial." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Hyperfactorial.html.

APA

Wolfram Language. (2008). Hyperfactorial. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Hyperfactorial.html

BibTeX

@misc{reference.wolfram_2024_hyperfactorial, author="Wolfram Research", title="{Hyperfactorial}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/Hyperfactorial.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_hyperfactorial, organization={Wolfram Research}, title={Hyperfactorial}, year={2008}, url={https://reference.wolfram.com/language/ref/Hyperfactorial.html}, note=[Accessed: 22-November-2024 ]}