Hyperfactorial

Hyperfactorial[n]

给出超阶乘函数 TemplateBox[{n}, Hyperfactorial].

更多信息

  • 数学函数，同时适合符号和数值运算.
  • 超阶乘函数对于正整数 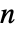定义为 TemplateBox[{n}, Hyperfactorial]=product_(k=1)^nk^k ，不然则定义为 TemplateBox[{z}, Hyperfactorial]=(z/(sqrt(2 pi)))^z exp(1/2 z (z-1)+TemplateBox[{{-, 2}, z}, PolyGamma2]).
  • 超阶乘函数满足 TemplateBox[{z}, Hyperfactorial]=z^z TemplateBox[{{z, -, 1}}, Hyperfactorial].
  • Hyperfactorial 可求任意数值精度的值.
  • Hyperfactorial 自动逐项作用于列表.

范例

打开所有单元关闭所有单元

基本范例  (5)

数值化计算：

在实数的子集上绘图：

在复数的子集上绘图：

在原点的级数展开：

在 Infinity 的级数展开：

范围  (28)

数值计算  (6)

数值化计算：

高精度计算：

输出的精度与输入的精度一致：

复数输入：

高精度的高效计算：

用 Around 计算一般情况下的统计区间：

计算数组中每个元素的值：

或用 MatrixFunction 计算矩阵形式的 Hyperfactorial 函数：

特殊值  (4)

在固定点的值：

零处的值：

Hyperfactorial 给出了 1/2 和 1/4 的整数倍的精确值：

求正极小值：

可视化  (2)

绘制 Hyperfactorial 的函数：

绘制 TemplateBox[{z}, Hyperfactorial] 实部：

绘制 TemplateBox[{z}, Hyperfactorial] 虚部：

函数属性  (11)

Hyperfactorial 的实域：

复数域：

在定义域上连续部分的 Hyperfactorial 函数值域：

Hyperfactorial 按元素线性作用于列表：

Hyperfactorial 不是解析函数：

也不是亚纯函数：

Hyperfactorial 既不是非递增，也不是非递减：

Hyperfactorial 不是单射函数：

Hyperfactorial 不是满射函数：

Hyperfactorial 既不是非负，也不是非正：

Hyperfactorial 在 x≤-1 时有奇点和断点：

Hyperfactorial 既不凸，也不凹：

TraditionalForm 格式化：

微分  (2)

关于 n 的一阶导：

关于 n 的高阶导：

绘制关于 n 的高阶导：

级数展开  (3)

使用 Series 求泰勒展开：

绘制 附近的前三个近似：

普通点的泰勒展开：

求在 Infinity 处的级数展开：

应用  (3)

用 Hyperfactorial 和 Exp 函数从极限中获取 Glaisher：

埃尔米特 (Hermite) 多项式的判别式和超阶乘相关：

较小阶数法里数列的所有非零元素的乘积：

与封闭式公式比较：

属性和关系  (3)

使用 FullSimplify 和 FunctionExpand 简化包含 Hyperfactorial 的表达式：

Product 转变成 Hyperfactorial：

FindSequenceFunction 可以识别 Hyperfactorial 序列：

巧妙范例  (2)

由二项式系数构成的矩阵的行列式：

由 Bernstein 多项式构建的矩阵的行列式：

Wolfram Research (2008)，Hyperfactorial，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Hyperfactorial.html.

文本

Wolfram Research (2008)，Hyperfactorial，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Hyperfactorial.html.

CMS

Wolfram 语言. 2008. "Hyperfactorial." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/Hyperfactorial.html.

APA

Wolfram 语言. (2008). Hyperfactorial. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Hyperfactorial.html 年

BibTeX

@misc{reference.wolfram_2024_hyperfactorial, author="Wolfram Research", title="{Hyperfactorial}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/Hyperfactorial.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_hyperfactorial, organization={Wolfram Research}, title={Hyperfactorial}, year={2008}, url={https://reference.wolfram.com/language/ref/Hyperfactorial.html}, note=[Accessed: 22-November-2024 ]}