Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

IncidenceMatrix

IncidenceMatrix[g]

给出图 g 的顶点-边关联矩阵.

IncidenceMatrix[{vw,…}]

使用规则 vw 指定图 g.

更多信息

IncidenceMatrix 也称为顶点-边入射矩阵.

IncidenceMatrix 返回一个 SparseArray 对象，该对象可以被 Normal 转化成一个普通矩阵.
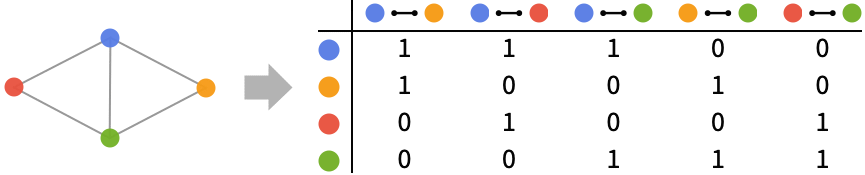
具有顶点 {v₁,…,v_n} 和边 {e₁,…,e_m} 的图的关联矩阵是元素为 a_ij 的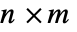矩阵，元素值由下列规则给出：
0 v_i 和 e_j 没有关联

1 e_j=v_iv_k、e_j=v_kv_i 或 e_j=v_kv_i

-1 e_j=v_iv_k

2 e_j=v_iv_i

-2 e_j=v_iv_i
假定顶点 v_i 的顺序由 VertexList[g] 给出，而边 e_j 的顺序由 EdgeList[g] 给出.

范例

打开所有单元关闭所有单元

基本范例 (2)

无向图的关联矩阵：

有向图的关联矩阵：

范围 (5)

无向图的关联矩阵没有负元素：

任意列中元素的和为 2：

有向图的关联矩阵含有一些负元素：

如果没有自环，则任意列的元素之和为 0：

具有自环的图的关联矩阵含有等于 2 的元素：

使用规则指定图：

IncidenceMatrix 适用于大规模的图：

使用 MatrixPlot 对矩阵进行可视化处理：

属性和关系 (9)

行和列分别与 VertexList 和 EdgeList 的顺序对应：

第行给出了所有与第个顶点相关联的边：

第一个顶点与边 2、3 和 4 相关联：

第列给出所有与第条边相关联的顶点索引：

第二条边与顶点 1 和 3 关联：

使用 VertexIndex 和 EdgeIndex 查找顶点和边的索引：

关联矩阵可以判别一个顶点或者一条边是否关联：

有向图的关联矩阵用表示源顶点，用表示目标顶点：

使用 DirectedGraph 计算无向图的有向关联矩阵：

使用随机方向的有向关联矩阵：

关联矩阵的大小由 VertexCount 和 EdgeCount 给出：

用 IncidenceGraph 从一个关联矩阵构建图：

一个线图的邻接矩阵可以用 IncidenceMatrix 计算：

顶部