WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

InverseWeierstrassP[p,{g2,g3}]

p に等しいワイエルシュトラス関数 の u の値を返す．

詳細
Details and Options Details and Options
例題  
例  
スコープ  
数値評価  
特定の値  
可視化  
Show More Show More
関数の特性  
微分  
積分  
級数展開  
一般化と拡張  
アプリケーション  
特性と関係  
考えられる問題  
関連項目
テクニカルノート
関連するガイド
関連リンク
履歴
引用書式

InverseWeierstrassP

InverseWeierstrassP[p,{g2,g3}]

p に等しいワイエルシュトラス関数 の u の値を返す．

詳細

  • 記号操作・数値操作の両方に適した数学関数である．
  • 返される u の値は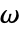， と 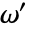により定義される基本周期平行四辺形の中に必ず存在する．
  • InverseWeierstrassP[{p,q},{g2,g3}]は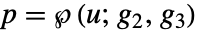，で 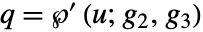とする u の値を求める．このような値が存在するためには，p と q は 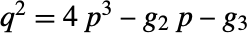の式を満たさなければならない．
  • InverseWeierstrassPは任意の数値精度で評価できる．

例題

すべて開く すべて閉じる

例  (4)

数値的に評価する：

Wolfram Language code: InverseWeierstrassP[2., {1, 2}]//Chop
Wolfram Language code: WeierstrassP[%, {1, 2}]

実数の部分集合上でプロットする：

Wolfram Language code: Plot[InverseWeierstrassP[x, {1, 2}], {x, 2, 6}]

複素数の部分集合上でプロットする：

Wolfram Language code: ComplexPlot3D[InverseWeierstrassP[z, {1, 2}], {z, -2 - 2I, 2 + 2I}, PlotLegends -> Automatic]

原点における級数展開：

Wolfram Language code: Series[InverseWeierstrassP[x, {1, 2}], {x, 0, 5}]

スコープ  (20)

数値評価  (4)

数値的に評価する：

Wolfram Language code: InverseWeierstrassP[7., {1, 2}]
Wolfram Language code: InverseWeierstrassP[11., {3, 2}]

高精度で評価する：

Wolfram Language code: N[InverseWeierstrassP[1 / 3, {1, 2}], 50]

出力精度は入力精度に従う：

Wolfram Language code: InverseWeierstrassP[3.222222222222222222222, {1, 2}]

複素数入力：

Wolfram Language code: InverseWeierstrassP[3. + I, {I, I + 2}]

高精度で効率的に評価する：

Wolfram Language code: InverseWeierstrassP[16`100, {3, 2}]//Timing
Wolfram Language code: InverseWeierstrassP[15`10000, {4, 2}];//Timing//Quiet

特定の値  (4)

固定点における値：

Wolfram Language code: Table[InverseWeierstrassP[x, {0, 0}], {x, {-1, 2}}]

ゼロにおける値：

Wolfram Language code: InverseWeierstrassP[0, {0, 0}]

InverseWeierstrassP[x,{1,2}]=2となるような x の値を求める：

Wolfram Language code: xval = x /. FindRoot[InverseWeierstrassP[x, {1, 2} ] == 2, {x, 3}]//Chop
Wolfram Language code: Plot[InverseWeierstrassP[x, {1, 2} ], {x, 1, 5}, Epilog -> Style[Point[{xval, InverseWeierstrassP[xval, {1, 2} ]}], PointSize[Large], Red]]

TraditionalFormによる表示：

Wolfram Language code: InverseWeierstrassP[z, {Subscript[g, 2], Subscript[g, 3]}]//TraditionalForm

可視化  (2)

InverseWeierstrassP関数をさまざまなパラメータについてプロットする：

Wolfram Language code: Plot[{InverseWeierstrassP[u, {2, 3}], InverseWeierstrassP[u, {4, 3}], InverseWeierstrassP[u, {4, 5}]}, {u, 1, 4}]

TemplateBox[{z, 7, 1}, InverseWeierstrassP]の実部をプロットする：

Wolfram Language code: ComplexContourPlot[Re[InverseWeierstrassP[z, {7, 1}]], {z, -3 - 3 I, 3 + 3I}, Contours -> 20]

TemplateBox[{z, 7, 1}, InverseWeierstrassP]の虚部をプロットする：

Wolfram Language code: ComplexContourPlot[Im[InverseWeierstrassP[z, {7, 1}]], {z, -3 - 3 I, 3 + 3I}, Contours -> 20]

関数の特性  (4)

InverseWeierstrassPは特異点と不連続点の両方を持つ：

Wolfram Language code: FunctionSingularities[InverseWeierstrassP[x, {1, 2}], x]//Quiet
Wolfram Language code: FunctionDiscontinuities[InverseWeierstrassP[x, {1, 2}], x]//Quiet

TemplateBox[{x, 1, 2}, InverseWeierstrassP]は単射である：

Wolfram Language code: FunctionInjective[InverseWeierstrassP[x, {2, 1}], x]
Wolfram Language code: Plot[{InverseWeierstrassP[x, {2, 1}], 2}, {x, 0, 6}]

TemplateBox[{x, 1, 2}, InverseWeierstrassP]は非負でも非正でもない：

Wolfram Language code: FunctionSign[InverseWeierstrassP[x, {1, 2}], x]

実軸上の一部では複素数値である：

Wolfram Language code: InverseWeierstrassP[0, {1, 2}]//N

TemplateBox[{x, {1, /, 2}, {1, /, 2}}, InverseWeierstrassP]は凸でも凹でもない：

Wolfram Language code: FunctionConvexity[InverseWeierstrassP[x, {1 / 2, 1 / 2}], x]

実軸上の一部では複素数値である：

Wolfram Language code: InverseWeierstrassP[0, {1 / 2, 1 / 2}]//N

微分  (2)

についての一次導関数：

Wolfram Language code: D[InverseWeierstrassP[p, {Subscript[``g``, 2], Subscript[``g``, 3]}], p]

についての高次導関数：

Wolfram Language code: Table[D[InverseWeierstrassP[p, {Subscript[``g``, 2], Subscript[``g``, 3]}], {p, k}], {k, 1, 4}]//FullSimplify

で のとき， についての高次導関数をプロットする：

Wolfram Language code: Plot[Evaluate[% /. {Subscript[``g``, 2] -> 1, Subscript[``g``, 3] -> 2}], {p, 1, 5}, PlotLegends -> {"First Derivative", "Second Derivative", "Third Derivative", "Fourth Derivative"}]

積分  (2)

Integrateを使って不定積分を計算する：

Wolfram Language code: Integrate[InverseWeierstrassP[x, {g2, g3}], x]

不定積分を確かめる：

Wolfram Language code: FullSimplify[D[%, x]]

定積分：

Wolfram Language code: Integrate[InverseWeierstrassP[x, {2, 3}], {x, 0, 5}]

級数展開  (2)

Seriesを使ってテイラー(Taylor)展開を求める：

Wolfram Language code: Series[InverseWeierstrassP[x, {g1, g2}], {x, 0, 2}]//Normal

の周りの最初の3つの近似をプロットする：

Wolfram Language code: terms = Abs@Normal@Table[Series[InverseWeierstrassP[x, {1, 2}], {x, 0, m}], {m, 1, 5, 2}]; Plot[{InverseWeierstrassP[x, {1, 2}], terms}, {x, 0, 7}]

生成点におけるテイラー展開：

Wolfram Language code: Series[InverseWeierstrassP[x, {g1, g2}], {x, x0, 2}]//Normal// FullSimplify

一般化と拡張  (1)

一般化された形を数値的に評価する：

Wolfram Language code: {p, pp} = {2., 2Sqrt[7]};
Wolfram Language code: z = InverseWeierstrassP[{p, pp}, {1, 2}]

以下はWeierstrassPとWeierstrassPPrimeの逆関数の関係である：

Wolfram Language code: p == WeierstrassP[z, {1, 2}]
Wolfram Language code: pp == WeierstrassPPrime[z, {1, 2}]

アプリケーション  (2)

InverseWeierstrassPの実部と虚部をプロットする：

Wolfram Language code: Plot[{Re[InverseWeierstrassP[x, {1, I}]], Im[InverseWeierstrassP[x, {1, I}]]}, {x, -2, 2}]

導関数を形成する：

Wolfram Language code: D[InverseWeierstrassP[z, {Subscript[g, 2], Subscript[g, 3]}], {z, 6}]//TraditionalForm

特性と関係  (1)

InverseWeierstrassPはEllipticLog関数と密接な関係がある：

Wolfram Language code: ellipticLog[{x_, y_}, {a_, b_}] := (1/2)InverseWeierstrassP[{(1/4)(x + (a/3)), (y/4)}, {(1/4)((a^2/3) - b), (1/8)(a/3)((b/2) - ((a/3))^2)}]

数値的に評価する：

Wolfram Language code: a = 3;b = 2; {x, y} = EllipticExp[1.2, {a, b}];
Wolfram Language code: ellipticLog[{x, y}, {a, b}]

組込み関数の値と比較する：

Wolfram Language code: EllipticLog[{x, y}, {a, b}]

考えられる問題  (2)

第1引数がワイエルシュトラス 関数の値のペアを表さない場合，InverseWeierstrassPは評価されずに残る：

Wolfram Language code: InverseWeierstrassP[{RandomReal[], RandomReal[]}, {1, 2}]

InverseWeierstrassPは，ベクトル値の第1引数で評価できる：

Wolfram Language code: InverseWeierstrassP[WeierstrassP[2, {1, 2}], {1, 2}]
Wolfram Research (1996), InverseWeierstrassP, Wolfram言語関数， https://reference.wolfram.com/language/ref/InverseWeierstrassP.html.

テキスト

Wolfram Research (1996), InverseWeierstrassP, Wolfram言語関数， https://reference.wolfram.com/language/ref/InverseWeierstrassP.html.

CMS

Wolfram Language. 1996. "InverseWeierstrassP." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/InverseWeierstrassP.html.

APA

Wolfram Language. (1996). InverseWeierstrassP. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InverseWeierstrassP.html

BibTeX

@misc{reference.wolfram_2026_inverseweierstrassp, author="Wolfram Research", title="{InverseWeierstrassP}", year="1996", howpublished="\url{https://reference.wolfram.com/language/ref/InverseWeierstrassP.html}", note=[Accessed: 04-November-2026]}

BibLaTeX

@online{reference.wolfram_2026_inverseweierstrassp, organization={Wolfram Research}, title={InverseWeierstrassP}, year={1996}, url={https://reference.wolfram.com/language/ref/InverseWeierstrassP.html}, note=[Accessed: 04-November-2026]}