WOLFRAM

Wolfram 语言与系统参考资料中心

InverseWeierstrassP[p,{g2,g3}]

给出使 Weierstrass 函数 等于 p 的 u 值.

更多信息
Details and Options Details and Options
范例  
基本范例  
范围  
数值计算  
特殊值  
可视化  
Show More Show More
函数的属性  
微分  
积分  
级数展开  
推广和延伸  
应用  
属性和关系  
可能存在的问题  
参见
技术笔记
相关指南
相关链接
历史
按以下格式引用：

InverseWeierstrassP

InverseWeierstrassP[p,{g2,g3}]

给出使 Weierstrass 函数 等于 p 的 u 值.

更多信息

  • 数学函数，适宜于符号和数值运算.
  • 返回的 u 值位于复半周期 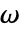和 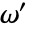定义的基本周期平行四边形中.
  • InverseWeierstrassP[{p,q},{g2,g3}] 求 u 的唯一值，其中 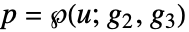和 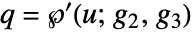. 若要此值存在，p 和 q 之间的关系需满足 .
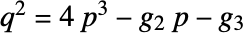  • InverseWeierstrassP 可求任意数值精度的值.

范例

打开所有单元 关闭所有单元

基本范例  (4)

数值运算：

Wolfram Language code: InverseWeierstrassP[2., {1, 2}]//Chop
Wolfram Language code: WeierstrassP[%, {1, 2}]

在实数的子集上绘图：

Wolfram Language code: Plot[InverseWeierstrassP[x, {1, 2}], {x, 2, 6}]

在复数的子集上绘图：

Wolfram Language code: ComplexPlot3D[InverseWeierstrassP[z, {1, 2}], {z, -2 - 2I, 2 + 2I}, PlotLegends -> Automatic]

原点处的级数展开式：

Wolfram Language code: Series[InverseWeierstrassP[x, {1, 2}], {x, 0, 5}]

范围  (20)

数值计算  (4)

数值计算：

Wolfram Language code: InverseWeierstrassP[7., {1, 2}]
Wolfram Language code: InverseWeierstrassP[11., {3, 2}]

高精度计算：

Wolfram Language code: N[InverseWeierstrassP[1 / 3, {1, 2}], 50]

输出的精度与输入的精度一致：

Wolfram Language code: InverseWeierstrassP[3.222222222222222222222, {1, 2}]

复数输入：

Wolfram Language code: InverseWeierstrassP[3. + I, {I, I + 2}]

在高精度条件下高效进行计算：

Wolfram Language code: InverseWeierstrassP[16`100, {3, 2}]//Timing
Wolfram Language code: InverseWeierstrassP[15`10000, {4, 2}];//Timing//Quiet

特殊值  (4)

在固定点的值：

Wolfram Language code: Table[InverseWeierstrassP[x, {0, 0}], {x, {-1, 2}}]

零处的值：

Wolfram Language code: InverseWeierstrassP[0, {0, 0}]

求满足 InverseWeierstrassP[x,{1,2}]=2 的 x 值：

Wolfram Language code: xval = x /. FindRoot[InverseWeierstrassP[x, {1, 2} ] == 2, {x, 3}]//Chop
Wolfram Language code: Plot[InverseWeierstrassP[x, {1, 2} ], {x, 1, 5}, Epilog -> Style[Point[{xval, InverseWeierstrassP[xval, {1, 2} ]}], PointSize[Large], Red]]

TraditionalForm 格式：

Wolfram Language code: InverseWeierstrassP[z, {Subscript[g, 2], Subscript[g, 3]}]//TraditionalForm

可视化  (2)

绘制各种参数值的 InverseWeierstrassP 函数：

Wolfram Language code: Plot[{InverseWeierstrassP[u, {2, 3}], InverseWeierstrassP[u, {4, 3}], InverseWeierstrassP[u, {4, 5}]}, {u, 1, 4}]

绘制 TemplateBox[{z, 7, 1}, InverseWeierstrassP] 的实部：

Wolfram Language code: ComplexContourPlot[Re[InverseWeierstrassP[z, {7, 1}]], {z, -3 - 3 I, 3 + 3I}, Contours -> 20]

绘制 TemplateBox[{z, 7, 1}, InverseWeierstrassP] 的虚部：

Wolfram Language code: ComplexContourPlot[Im[InverseWeierstrassP[z, {7, 1}]], {z, -3 - 3 I, 3 + 3I}, Contours -> 20]

函数的属性  (4)

InverseWeierstrassP 既有奇点，也有断点：

Wolfram Language code: FunctionSingularities[InverseWeierstrassP[x, {1, 2}], x]//Quiet
Wolfram Language code: FunctionDiscontinuities[InverseWeierstrassP[x, {1, 2}], x]//Quiet

TemplateBox[{x, 1, 2}, InverseWeierstrassP] 是单射函数：

Wolfram Language code: FunctionInjective[InverseWeierstrassP[x, {2, 1}], x]
Wolfram Language code: Plot[{InverseWeierstrassP[x, {2, 1}], 2}, {x, 0, 6}]

TemplateBox[{x, 1, 2}, InverseWeierstrassP] 既不是非负，也不是非正：

Wolfram Language code: FunctionSign[InverseWeierstrassP[x, {1, 2}], x]

在部分实轴上的值是复数：

Wolfram Language code: InverseWeierstrassP[0, {1, 2}]//N

TemplateBox[{x, {1, /, 2}, {1, /, 2}}, InverseWeierstrassP] 既不凸，也不凹：

Wolfram Language code: FunctionConvexity[InverseWeierstrassP[x, {1 / 2, 1 / 2}], x]

在部分实轴上的值是复数：

Wolfram Language code: InverseWeierstrassP[0, {1 / 2, 1 / 2}]//N

微分  (2)

关于 的一阶导数：

Wolfram Language code: D[InverseWeierstrassP[p, {Subscript[g, 2], Subscript[g, 3]}], p]

关于 的高阶导数：

Wolfram Language code: Table[D[InverseWeierstrassP[p, {Subscript[``g``, 2], Subscript[``g``, 3]}], {p, k}], {k, 1, 4}]//FullSimplify

绘制 且 时关于 的高阶导数：

Wolfram Language code: Plot[Evaluate[% /. {Subscript[``g``, 2] -> 1, Subscript[``g``, 3] -> 2}], {p, 1, 5}, PlotLegends -> {"First Derivative", "Second Derivative", "Third Derivative", "Fourth Derivative"}]

积分  (2)

使用 Integrate 计算不定积分：

Wolfram Language code: Integrate[InverseWeierstrassP[x, {g2, g3}], x]

验证反导数：

Wolfram Language code: FullSimplify[D[%, x]]

定积分：

Wolfram Language code: Integrate[InverseWeierstrassP[x, {2, 3}], {x, 0, 5}]

级数展开  (2)

用 Series 求泰勒展开式：

Wolfram Language code: Series[InverseWeierstrassP[x, {g1, g2}], {x, 0, 2}]//Normal

绘制 附近的前三个近似式：

Wolfram Language code: terms = Abs@Normal@Table[Series[InverseWeierstrassP[x, {1, 2}], {x, 0, m}], {m, 1, 5, 2}]; Plot[{InverseWeierstrassP[x, {1, 2}], terms}, {x, 0, 7}]

普通点处的泰勒展开式：

Wolfram Language code: Series[InverseWeierstrassP[x, {g1, g2}], {x, x0, 2}]//Normal// FullSimplify

推广和延伸  (1)

数值式计算广义形式：

Wolfram Language code: {p, pp} = {2., 2Sqrt[7]};
Wolfram Language code: z = InverseWeierstrassP[{p, pp}, {1, 2}]

WeierstrassP 和 WeierstrassPPrime 存在相反关系：

Wolfram Language code: p == WeierstrassP[z, {1, 2}]
Wolfram Language code: pp == WeierstrassPPrime[z, {1, 2}]

应用  (2)

绘制 InverseWeierstrassP 的实部和虚部：

Wolfram Language code: Plot[{Re[InverseWeierstrassP[x, {1, I}]], Im[InverseWeierstrassP[x, {1, I}]]}, {x, -2, 2}]

形成导数：

Wolfram Language code: D[InverseWeierstrassP[z, {Subscript[g, 2], Subscript[g, 3]}], {z, 6}]//TraditionalForm

属性和关系  (1)

InverseWeierstrassP 与 EllipticLog 函数密切相关：

Wolfram Language code: ellipticLog[{x_, y_}, {a_, b_}] := (1/2)InverseWeierstrassP[{(1/4)(x + (a/3)), (y/4)}, {(1/4)((a^2/3) - b), (1/8)(a/3)((b/2) - ((a/3))^2)}]

用数值法计算：

Wolfram Language code: a = 3;b = 2; {x, y} = EllipticExp[1.2, {a, b}];
Wolfram Language code: ellipticLog[{x, y}, {a, b}]

与内置函数的值相比较：

Wolfram Language code: EllipticLog[{x, y}, {a, b}]

可能存在的问题  (2)

如果第一个参数不能表示 Weierstrass 函数的一对值，InverseWeierstrassP 保留不计算的形式:

Wolfram Language code: InverseWeierstrassP[{RandomReal[], RandomReal[]}, {1, 2}]

InverseWeierstrassP 计算结果的的第一个参数是向量：

Wolfram Language code: InverseWeierstrassP[WeierstrassP[2, {1, 2}], {1, 2}]
Wolfram Research (1996)，InverseWeierstrassP，Wolfram 语言函数，https://reference.wolfram.com/language/ref/InverseWeierstrassP.html.

文本

Wolfram Research (1996)，InverseWeierstrassP，Wolfram 语言函数，https://reference.wolfram.com/language/ref/InverseWeierstrassP.html.

CMS

Wolfram 语言. 1996. "InverseWeierstrassP." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/InverseWeierstrassP.html.

APA

Wolfram 语言. (1996). InverseWeierstrassP. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/InverseWeierstrassP.html 年

BibTeX

@misc{reference.wolfram_2026_inverseweierstrassp, author="Wolfram Research", title="{InverseWeierstrassP}", year="1996", howpublished="\url{https://reference.wolfram.com/language/ref/InverseWeierstrassP.html}", note=[Accessed: 05-August-2026]}

BibLaTeX

@online{reference.wolfram_2026_inverseweierstrassp, organization={Wolfram Research}, title={InverseWeierstrassP}, year={1996}, url={https://reference.wolfram.com/language/ref/InverseWeierstrassP.html}, note=[Accessed: 05-August-2026]}