



LaguerreL
Details

- Mathematical function, suitable for both symbolic and numerical manipulation.
- Explicit polynomials are given when possible.
![TemplateBox[{n, x}, LaguerreL]=TemplateBox[{n, 0, x}, LaguerreL3] TemplateBox[{n, x}, LaguerreL]=TemplateBox[{n, 0, x}, LaguerreL3]](Files/LaguerreL.en/3.png) .
. - The Laguerre polynomials are orthogonal with weight function
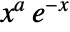 .
. - They satisfy the differential equation
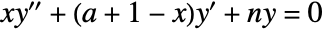 .
. - For certain special arguments, LaguerreL automatically evaluates to exact values.
- LaguerreL can be evaluated to arbitrary numerical precision.
- LaguerreL automatically threads over lists.
- LaguerreL[n,x] is an entire function of x with no branch cut discontinuities.
- LaguerreL can be used with Interval and CenteredInterval objects. »
Examples
open all close allBasic Examples (6)
Compute the 5![]() Laguerre polynomial:
Laguerre polynomial:
Compute the associated Laguerre polynomial ![]() :
:
Plot over a subset of the reals:
Plot over a subset of the complexes:
Series expansion at the origin:
Series expansion at Infinity:
Scope (41)
Numerical Evaluation (6)
The precision of the output tracks the precision of the input:
Evaluate efficiently at high precision:
Compute worst-case guaranteed intervals using Interval and CenteredInterval objects:
Or compute average-case statistical intervals using Around:
Compute the elementwise values of an array:
Or compute the matrix LaguerreL function using MatrixFunction:
Specific Values (5)
Visualization (3)
Plot the LaguerreL polynomial for various orders:
Function Properties (13)
The primary Laguerre function is defined for all real and complex values:
The associated Laguerre function ![]() has restrictions on
has restrictions on ![]() and
and ![]() , but not
, but not ![]() :
:
![]() achieves all real and complex values:
achieves all real and complex values:
LaguerreL has the mirror property ![]() :
:
LaguerreL threads elementwise over lists:
![]() is an analytic function of
is an analytic function of ![]() and
and ![]() :
:
![]() is not analytic, but it is meromorphic:
is not analytic, but it is meromorphic:
![]() is neither non-decreasing nor non-increasing:
is neither non-decreasing nor non-increasing:
Laguerre polynomials are not injective for values other than 1:
LaguerreL is neither non-negative nor non-positive:
![]() has no singularities or discontinuities in
has no singularities or discontinuities in ![]() :
:
TraditionalForm formatting:
Differentiation (3)
Integration (3)
Series Expansions (5)
Find the Taylor expansion using Series:
Plots of the first three approximations around ![]() :
:
General term in the series expansion using SeriesCoefficient:
Find the series expansion at Infinity:
Generalizations & Extensions (1)
LaguerreL can be applied to a power series:
Applications (6)
Solve the Laguerre differential equation:
Generalized Fourier series for functions defined on ![]() :
:
Radial wave-function of the hydrogen atom:
Compute the energy eigenvalue from the differential equation:
The energy is independent of the orbital quantum number l:
The number of derangement anagrams for a word with character counts ![]() :
:
Count the number of derangements for the word Mathematica:
Compare the value of the MarcumQ function for large arguments to its asymptotic formula:
Construct an approximation using the central limit theorem:
An n-point Gauss–Laguerre quadrature rule is based on the roots of the n![]() -order Laguerre polynomial. Compute the nodes and weights of an n-point Gauss–Laguerre quadrature rule for a given value of
-order Laguerre polynomial. Compute the nodes and weights of an n-point Gauss–Laguerre quadrature rule for a given value of ![]() :
:
Use the n-point Gaussian quadrature rule to numerically evaluate an integral:
Compare the result of the Gauss–Laguerre quadrature with the result from NIntegrate:
Properties & Relations (7)
Get the list of coefficients in a Laguerre polynomial:
Use FunctionExpand to expand LaguerreL functions into simpler functions:
LaguerreL can be represented as a DifferentialRoot:
LaguerreL can be represented in terms of MeijerG:
LaguerreL can be represented as a DifferenceRoot:
General term in the series expansion of LaguerreL:
The generating function for LaguerreL:
See Also
Tech Notes
Related Links
History
Introduced in 1988 (1.0) | Updated in 2021 (13.0) ▪ 2022 (13.1)
Text
Wolfram Research (1988), LaguerreL, Wolfram Language function, https://reference.wolfram.com/language/ref/LaguerreL.html (updated 2022).
CMS
Wolfram Language. 1988. "LaguerreL." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/LaguerreL.html.
APA
Wolfram Language. (1988). LaguerreL. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LaguerreL.html
BibTeX
@misc{reference.wolfram_2025_laguerrel, author="Wolfram Research", title="{LaguerreL}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/LaguerreL.html}", note=[Accessed: 03-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_laguerrel, organization={Wolfram Research}, title={LaguerreL}, year={2022}, url={https://reference.wolfram.com/language/ref/LaguerreL.html}, note=[Accessed: 03-March-2026]}