LogSeriesDistribution
母数 θ の対数級数分布を表す.
詳細
- LogSeriesDistributionは対数分布としても知られている.
- 対数級数分布における値
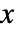 の確率は,正の整数については
の確率は,正の整数については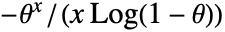 であり,その他の場合はゼロである. »
であり,その他の場合はゼロである. » - LogSeriesDistributionでは,θ は0から1までの任意の実数でよい.
- LogSeriesDistributionは,Mean,CDF,RandomVariate等の関数で使うことができる. »
予備知識
- LogSeriesDistribution[θ]は,整数値
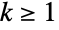 について定義され,
について定義され,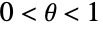 である実数母数 θ によって決定された離散統計分布を表す.対数級数分布の確率密度関数(PDF)は,離散的で単調減少である.この分布は,対数分布と呼ばれることがある.
である実数母数 θ によって決定された離散統計分布を表す.対数級数分布の確率密度関数(PDF)は,離散的で単調減少である.この分布は,対数分布と呼ばれることがある. - この分布は,動物集団のモデリングツールとして,英国人科学者のR. A. Fisherによる1943年の論文ではじめて論じられた.それ以来,この分布は,植物学,生存分析,金融等を含むさまざまな分野で使われてきた.対数級数分布は,人口増加のような大規模現象や一定期間に特定の個人が購入した製品数のような小規模行動の説明に特に有効である.この分布は,(Yule–Furry過程,線形出生死滅過程,Pólya過程のような確率過程との関係において)推計学で使われており,一科学の広範囲に渡る分野のさまざまな現象のモデル化にも般化されて使われている.
- RandomVariateを使って,対数級数分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,BetaDistribution[α,β]](より簡略な表記では xBetaDistribution[α,β])を使って,確率変数 x が対数級数分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[LogSeriesDistribution[θ],x]およびCDF[LogSeriesDistribution[θ],x]を使って得られる.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.これらの数量は,DiscretePlotを使って可視化することができる.
- DistributionFitTestを使って,与えられたデータ集合が対数級数分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータからパラメトリック対数級数分布を推定することが,FindDistributionParametersを使ってデータを対数級数分布にフィットすることができる.ProbabilityPlotを使って記号対数級数分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って記号対数級数分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換された対数級数分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使って対数級数分布を含む高次元分布を構築することが,ProductDistributionを使って対数級数分布を含む独立成分分布の結合分布を計算することができる.
- LogSeriesDistributionは,他の数多くの統計分布と関連している.LogSeriesDistributionは,適切に定義された母数 n および p について,CompoundPoissonDistribution[μ,LogSeriesDistribution[θ]]がNegativeBinomialDistribution[n,p]と等しいと
いう意味で,複合ポアソン分布と組み合せて使ってNegativeBinomialDistributionを得ることができる.したがって,LogSeriesDistributionはBinomialDistribution,MultinomialDistribution,NegativeMultinomialDistributionとも関連している.
例題
すべて開くすべて閉じるアプリケーション (2)
特性と関係 (2)
LogSeriesDistributionのあるCompoundPoissonDistributionの特殊ケース:
以下で定義された母数があると,![]() はNegativeBinomialDistributionである:
はNegativeBinomialDistributionである:
考えられる問題 (2)
Wolfram Research (2007), LogSeriesDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/LogSeriesDistribution.html.
テキスト
Wolfram Research (2007), LogSeriesDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/LogSeriesDistribution.html.
CMS
Wolfram Language. 2007. "LogSeriesDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/LogSeriesDistribution.html.
APA
Wolfram Language. (2007). LogSeriesDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LogSeriesDistribution.html