MovingMap

MovingMap[f,data,w]

data で指定されたサイズ w の窓に f を適用する．

MovingMap[f,data,wspec]

wspec で指定された窓を使う．

MovingMap[f,data,wspec,padding]

padding を使って data を充填する．

詳細

  • MovingMapは，規則的な間隔のデータと不規則間隔のデータに使うことができる．
  • 多くのコンテキストにおいて，tiは時点を表す．
  • data は，値のリスト{x1,x2,…}，時点と値のペアのリスト{{t1,x1},{t2,x2},…}，TimeSeries，EventSeries，TemporalDataのいずれかでよい，
  • 1引数の関数 f が，各窓の値のリスト{xi,xi+1,…}に適用される． »
  • 純関数 f は，次の引数を使って，各窓についての値，時，境界値，境界時間にアクセスすることができる． »
  • #Values または #1窓内のデータ値
    #Times または #2窓内のデータ時点
    #BoundaryValues または #3窓の境界でリサンプルされた値
    #BoundaryTimes または #4窓の境界の時点
    #Dates または #5窓内のデータの日付
  • デフォルトで，f は各窓について1つの値を計算し，時点は自動的に計算されると期待される．出力を規則{τi,…}{vi,…}として与える関数 f を使うと，時点と値を制御するとともに，1つの窓について複数の値を作成することができる． »
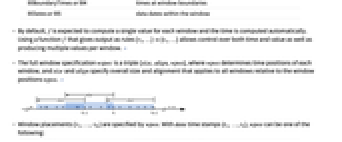
  • 完全な窓指定 wspec は3つ1組の{size,align,wpos}である．ただし，wpos は各窓の時点位置を定義し，size および align は窓位置 wpos で取り出されるすべての窓に適用される全体的な大きさと並べ方を指定する． »
  • 窓のパラメータ{τ1,…,τm} は wpos に特有である．data のタイムスタンプが{t1,…,tn}のとき，wpos は，次のいずれかである．
  • Automaticdata タイムスタンプ τi=tiを使う
    {τmin,τmax}τmin≤tk+i≤τmaxとなるような τi=tk+iを使う
    {Automatic,τmax}{t1,τmax}に等しい
    {τmin,Automatic}{τmin,tn}に等しい
    {τmin,τmax,dτ}τ1=τmin，τ2=τmin+dτ 等を使う
    {{τ1,…,τm}}明示的な τ1，τ2等を使う
  • デフォルトで，出力のタイムスタンプは{τ1,…,τm}である．
  • 窓の size は以下で与えることができる．
  • w正の数，日数を表すとみなされる
    Quantity[w,timeunit]継続時間 w（単位：timeunit）
    Quantity[n,"Events"]窓の大きさを定義する事象数 n
  • 窓の大きさは，相対単位"Month"あるいは"Events"に言及している際に，絶対的な意味で変わることがある．
  • 窓の並べ方 align は，窓内の τiの相対位置を決定する．使用可能な設定値には，Right（デフォルト），Left，Centerがある．
  • 窓指定{size,align}は{size,align,Automatic}に等しい．
  • 窓指定 size あるいは{size}は{size,Right,Automatic}に等しい．
  • padding の設定値
  • Automaticオーバーハングしない窓だけを保存する（デフォルト）
    None充填はせず，すべての窓を保存する
    valuepadding{Automatic,valuepadding}に等しい
    {timepadding,valuepadding}時点と値の充填設定
  • valuepadding の設定値は，ArrayPadが認識する任意の有効な指定でよい．
  • timepadding の設定
  • Automatic時点 - 刻み幅の中央値ので一様に
    Δt刻み幅 Δt で一様に
    {Δt1,Δt2,…}ステップ Δtiで循環的に充填
    "ReflectedDifferences"時点間の差の反映
    "PeriodicDifferences"ステップ ti+1-tiで循環的に充填
  • MovingMapは，複数の経路がある data については，経路ごとに縫い込まれる．

例題

すべて開くすべて閉じる

例  (3)

幅2の窓を平均する：

3要素の移動平均を行う：

間隔が不規則な時系列を平滑化する：

月ごとの区間で窓を定期的に置く：

複数の経路を同時に平滑化する：

中揃えの離散窓と鏡映充填を使う：

スコープ  (30)

基本的な用法  (4)

関数 f を時点2単位の幅の窓があるデータにマップする：

関数 f を，3事象の窓のデータにマップする：

データの移動変位値を計算する：

単位サイズの中心窓を使う：

移動変位値の包絡線を求める：

SP500時系列の1年間の移動平均を求める：

窓を月ごとに置いて，時系列の1年間の移動平均を求める：

窓を月ごとに各月の1日に置いて，反映される値の充填を使う：

データの型  (7)

ベクトルについての一般的な移動関数を作る：

時点と値のペアのリストについての移動平均を計算する：

TimeSeriesについての移動GeometricMeanを計算する：

TemporalDataについての移動中央値を計算する：

EventSeriesについての移動合計を計算する：

複数の経路についての移動分散を同時に計算する：

二変量時系列の2成分間の移動相関係数を計算する：

サイズ100の窓上の移動相関係数：

関数  (5)

汎用関数を移動窓内の値に適用する：

代りに，純関数を使う：

汎用関数を移動窓内の値とタイムスタンプに適用する：

名前付きの引数を持つ純関数を使う：

境界時間と境界時間におけるリサンプルされた値を持つ関数も与える：

各窓について時点と値の両方を計算する関数を定義する：

これを使って，事実上，窓の平均と窓内のスケールされた時点を関連させる：

欠測値と対応する時点を削除する関数を定義する：

イリノイ州シャンペーンの気温：

欠測値を含む時系列：

欠測値のデータ点を削除する：

1月の平均気温を計算する：

感謝祭の連休の日数を求める：

窓の大きさ  (4)

移動窓の数値による幅を使う：

時間量を使って移動窓の程度を指定する：

ペア{n,"unit"}を使って窓のサイズを指定する：

4時間ごとに1日の気温の中央値を求める：

季節ごとの気温の四分位数を示し，時系列を可視化する：

窓サイズを，含まれている事象数で指定する：

1週間の事象数の移動平均を求める：

窓揃え  (4)

右揃えの窓は過去の値を使う：

デフォルトで，右揃えが使われる：

中央揃えの窓は過去と未来の値を使う：

左揃えの窓は未来の値を使う：

窓の揃え方を比べる：

時系列は規則的なので，各整列法についての移動平均の値は等しい：

時点はそうではない：

視覚的比較：

窓の置き方  (3)

各データ点に自動的に窓を置く：

区間内のすべてのデータ点に窓を置く：

指定された例の後ろの各データ点に窓を置く：

窓を一様に置く：

指定された範囲内に窓を一様に置く：

指定されたタイムスタンプに窓を置く：

関心のある各日付について，過去2四半期内の最高株価を求める：

充填  (3)

Automatic充填の場合データの時間領域にオーバーハングしない窓だけが使われる：

デフォルトではAutomatic充填が使われる：

充填をNoneに設定すると，データの時間領域が重なり合う窓が出る：

Automaticの時間充填と一定の値の充填を使う：

アプリケーション  (10)

平滑化データと間伐データ  (1)

イリノイ州サボイにおけるバレンタインデー付近の解像度が約1分の気温の記録：

解像度を20分にして，1時間ごとの移動平均を計算する：

市場のボラティリティ  (1)

S&P 500のボラティリティが高い期間を特定する：

5年間の移動平均偏差：

年ごとの移動四分位間範囲：

2年間の移動範囲：

加重移動平均  (3)

最近の値により重みを置いて，規則的な時系列の移動平均を計算する：

過去の値により重みを置いた場合と比較する：

中央揃えの窓を使い，最大の重みを中央値に置く：

不規則な連続時系列の移動時間平均を計算する：

領域内の，線形補間関数の積分の重み：

区間{t1,tn}内の{{t1,v1},…,{tn,vn}}の線形補間の時間平均：

粒子軌道  (2)

裾部が重い測定ノイズで軌道のシミュレーションを行う：

もとになっている信号とノイズを含むシミュレーションによる経路：

移動TrimmedMeanを使って軌道を平滑化する：

窓サイズを大きくすると，滑らかな軌道が得られる：

3D空間で測定ノイズを含むオブジェクトの軌道を平滑化する：

GARCH過程およびARMA過程  (1)

GARCH（一般化された条件付き分散不均一自己回帰）過程とARMA（自己回帰移動平均）過程のボラティリティを比較する：

定常平均および分散はこれらの過程について等しい：

GARCH過程については，ボラティリティは特徴的な峰を示す：

時系列フィルタ  (1)

イリノイ州サボイにおける，バレンタインデー付近のマルチ解像度の気温の記録：

窓内の最高気温の時点と値を求める関数を指定する：

窓内の最低気温の時点と値を求める関数を指定する：

各日の午前零時に，1日長，左揃えの窓を指定する：

時点変更ウィナー過程  (1)

WienerProcessのサンプルからOrnsteinUhlenbeckProcessのサンプルを構築する：

を使い，および から および を求める：

1つの事象窓上で，ウィナー経路の時点と値のペアをOrnstein–Uhlenbeck経路の時点と値のペアにマップする，移動マップを計算する：

経路のシミュレーションを可視化し，過程の平均値関数と比較する：

特性と関係  (5)

規則的なデータ上のMeanのMovingMapはMovingAverageに等しい：

規則的なデータ上のMedianのMovingMapはiMovingMedianに等しい：

MovingMapはListConvolveに関連している：

MovingMapはListCorrelateに関連している：

逐次差分を取る：

Differencesを使うこともできる：

より高次の差分に一般化する：

おもしろい例題  (2)

大域的MinおよびMaxを求める：

合衆国憲法中のエントロピーの変化を可視化する．同じ単語が繰り返し使われている場合はエントロピーが低くなる：

数名が自分の名前と出身州をリストする箇所でエントロピーが高くなる：

大統領の継承に関する米国憲法修正第25条は，比較的繰り返しが多い：

修正第25条で最も頻繁に繰り返される10の単語：

Wolfram Research (2014), MovingMap, Wolfram言語関数， https://reference.wolfram.com/language/ref/MovingMap.html （2017年に更新）.

テキスト

Wolfram Research (2014), MovingMap, Wolfram言語関数， https://reference.wolfram.com/language/ref/MovingMap.html （2017年に更新）.

CMS

Wolfram Language. 2014. "MovingMap." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/MovingMap.html.

APA

Wolfram Language. (2014). MovingMap. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MovingMap.html

BibTeX

@misc{reference.wolfram_2024_movingmap, author="Wolfram Research", title="{MovingMap}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/MovingMap.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_movingmap, organization={Wolfram Research}, title={MovingMap}, year={2017}, url={https://reference.wolfram.com/language/ref/MovingMap.html}, note=[Accessed: 22-November-2024 ]}