MovingMap

MovingMap[f,data,w]

在给定 data 中，对大小为 w 的窗口应用 f.

MovingMap[f,data,wspec]

使用指定窗口 wspec.

MovingMap[f,data,wspec,padding]

用 padding 来填充 data.

更多信息

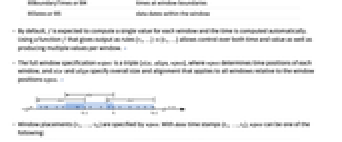
MovingMap 可用于规则间隔和不规则间隔的数据.

许多情况下，t_i 是时间.
data 可以是数值列表 {x₁,x₂,…}，一组时间-数值对 {{t₁,x₁},{t₂,x₂},…}，一个 TimeSeries，EventSeries 或 TemporalData.
将单变量函数 f 应用到每个窗口的数值列表 {x_i,x_i+1,…}. »
利用下列参数，纯函数 f 可以访问每个窗口的数值、时间、边界值，以及边界时间： »

	#Values or #1	窗口内的数值数据
	#Times or #2	窗口内的时间数据
	#BoundaryValues or #3	窗口边界处重新抽样的值
	#BoundaryTimes or #4	窗口边界处的时间
	#Dates or #5	窗口内的数据日期

缺省情况下，对于每个窗口，f 算出一个数值，时间则是自动算出的. 使用输出为规则 {τ_i,…}{v_i,…} 的函数 f 则允许同时控制时间和数值，每个窗口还可以产生多个数值. »
窗口规范 wspec 的形式为 {size,align,wpos}，其中 wpos 确定了每个窗口的时间位置，size 和 align 则指定了窗口的大小和所有窗口相对于 wpos 的对齐方式. »

窗口位置 {τ₁,…,τ_m} 由 wpos 指定. 如果 data 的时间戳为 {t₁,…,t_n}，wpos 可采用以下任意一种设置：

	Automatic	使用 data 的时间戳，τ_i=t_i
	{τ_min,τ_max}	τ_i=t_k+i，以使 τ_min≤t_k+i≤τ_max
	{Automatic,τ_max}	相当于 {t₁,τ_max}
	{τ_min,Automatic}	相当于 {τ_min,t_n}
	{τ_min,τ_max,dτ}	τ₁=τ_min，τ₂=τ_min+dτ，以此类推
	{{τ₁,…,τ_m}}	明确指定 τ₁, τ₂ ......

缺省情况下，输出的时间戳为 {τ₁,…,τ_m}.
窗口大小 size 可以为：
w 正数，指的是天

Quantity[w,timeunit] 时长为 w ，单位为 timeunit

Quantity[n,"Events"] 用事件计数 n 来定义窗口大小
当参照单位为 "Month" 或 "Events" 时，窗口大小的具体数值可能会改变.
窗口的对齐方式 align 确定了窗口内 τ_i 的相对位置. 可能的设置包括 Right（缺省值），Left 和 Center.

窗口规范 {size,align} 等价于 {size,align,Automatic}.
窗口规范 size 或 {size} 等价于 {size,Right,Automatic}.
padding 的设置包括：

	Automatic	只保留没有外伸的窗口（缺省）
	None	不填充，保留所有窗口
	valuepadding	等价于 {Automatic,valuepadding}
	{timepadding,valuepadding}	时间和数值的填充设置

valuepadding 的设置可以是能被 ArrayPad 识别的任意有效规范.
timepadding 的设置包括：

	Automatic	用时间步长大小的中值均匀填充
	Δt	用步长大小 Δt 均匀填充
	{Δt₁,Δt₂,…}	循环使用 Δt_i 来填充
	"ReflectedDifferences"	使用时间之差的映射来填充
	"PeriodicDifferences"	循环使用 t_i+1-t_i 来填充

对于多路径 data，MovingMap 会对各个路径分别进行计算.

范例

打开所有单元关闭所有单元

基本范例 (3)

窗口宽度为2，进行平均计算：

进行三个元素的移动平均计算：

平滑一个不规则间隔的时间序列：

以月为区间单位有规律地放置窗口：

同时平滑多条路径：

采用居中对齐的窗口以及映射填充：

范围 (30)

基本用途 (4)

窗口宽度为两个时间单位，将函数 f 运用到窗口内的数据上：

窗口宽度为三个事件，将函数 f 运用到窗口内的数据上：

计算数据的移动分位数：

使用大小为一个单位的居中对齐的窗口：

求移动四分位数包络线：

计算 SP500 时间序列的年度移动平均：

按月放置窗口，计算时间序列的年度移动平均：

在每个月的第一天按月放置窗口，用映射数据的方式来填充：

数据类型 (7)

生成一个矢量的通用移动函数：

计算一组时间-数值对的移动平均值：

计算一个 TimeSeries 的移动 GeometricMean：

计算 TemporalData 的移动中值：

计算一个 EventSeries 的移动总和：

同时计算多条路径的移动方差：

计算一个的双变量时间序列两个分量之间的移动相关系数：

窗口大小为100，得出的移动相关系数为：

函数 (5)

将一个通用函数运用到移动窗口内的数值上：

使用纯函数：

将一个通用函数运用到移动窗口内的数值和时间戳上：

使用带有命名参数的纯函数：

同时将边界时间和边界时间处重新抽样的值提供给函数：

定义一个函数来计算每个窗口的时间和数值：

用它将窗口的平均值和窗口内缩放过的时间点有效的结合起来：

定义一个函数，去掉缺失的值及对应的时间：

伊利诺伊洲香槟市的温度读数：

时间序列中含有一些缺失值：

将含有缺失值的数据点删掉：

计算一月份的平均温度：

查找连续感恩节之间的天数：

窗口大小 (4)

用数字宽度指定移动窗口的大小：

用时间量指定移动窗口的范围：

用 {n,"unit"} 来指定窗口大小：

求每天每4个小时的温度中值：

可视化时间序列，显示季节性温度四分位数：

按包含的事件数指定窗口大小：

求每周事件数目的移动平均值：

窗口对齐方式 (4)

向右对齐的窗口使用过去的数据：

缺省情况下，使用向右对齐：

居中对齐的窗口同时使用过去及将来的数据：

向左对齐的窗口使用将来的数据：

比较不同的窗口对齐方式：

因为时间序列是规则的，用不同的对齐方式计算数值的移动平均，结果是一样的：

而时间结果则不同：

图示结果进行比较：

窗口放置方式 (3)

自动将窗口放在每个数据点上：

将窗口放在一个区间内的每个数据点上：

在某个给定时刻之后将窗口放在每个数据点上：

均匀放置窗口：

在给定范围内均匀放置窗口：

将窗口放置在给定时间戳上：

对于每个感兴趣的日期，找出过去两个季度内股票的最高值：

填充 (3)

填充方式设置为 Automatic 时，只使用那些没有超过数据时间范围的窗口：

缺省情况下，填充方式设置为 Automatic：

当填充方式设置为 None 时，有些窗口会越过数据的时间范围：

时间填充方式为 Automatic，而数据则用常数填充：

应用 (10)

数据平滑和抽稀 (1)

情人节前后，伊利诺伊洲 Savoy 市的温度读数，每分钟取得一个数据：

每隔20分钟计算一小时的移动平均值：

市场波动 (1)

找出标普500大幅波动的时期:

五年移动标准差：

年移动四分位距：

二年内的变动范围：

加权移动平均 (3)

计算规则时间序列的移动平均，给最近的值更多权重：

和给过去的值更多权重的情况比较：

使用居中对齐窗口，给中间的值更多权重：

计算不规则抽样的连续时间序列的移动时间平均：

域内线性插值函数的积分的权重：

区间 {t₁,t_n} 上 {{t₁,v₁},…,{t_n,v_n}} 的线性插值的时间平均：

粒子轨迹 (2)

模拟一条带有重尾测量噪声的轨迹：

基本信号和带有噪声的模拟路径：

用移动 TrimmedMean 来平滑轨迹：

增大窗口宽度使得轨迹更平滑：

平滑一个物体在三维空间内带有测量噪声的轨迹：

GARCH 和 ARMA 过程 (1)

比较 GARCH 和 ARMA 过程的波动率：

两个过程的稳态平均和方差相同：

对于 GARCH 过程，波动率呈现出特征性尖峰：

时间序列滤波器 (1)

情人节前后，伊利诺伊洲 Savoy 市每分钟的温度读数：

指定一个函数来找出窗口内温度的最高值及时间：

指定一个函数来找出窗口内温度的最低值及时间：

窗口长度为1天，左对齐，将窗口放置在每天开始的时间：

时间变换维纳过程 (1)

根据 WienerProcess 的样本构建 OrnsteinUhlenbeckProcess 的样本：

使用，根据和计算和：

在长度为一个事件的窗口内，计算函数的移动映射，该函数将维纳路径时间-数值对映射至 Ornstein–Uhlenbeck 路径时间-数值对：

可视化模拟路径并和过程平均函数进行比较：

属性和关系 (5)

规则数据的 Mean 的 MovingMap 等价于 MovingAverage：

规则数据的 Median 的 MovingMap 等价于 MovingMedian：

MovingMap 和 ListConvolve 有关：

MovingMap 和 ListCorrelate 有关：

取连续差：

还可以用 Differences：

推广至高阶差：

巧妙范例 (2)

求移动全局 Min 和 Max：

查看美国宪法中的熵变. 重复使用同一个词时熵值较低：

在几个人列出他们的名字和所属的州处，熵值出现一个峰值：

第25修正案，关于总统连任的部分，重复性较高：

在第25修正案中，出现频率最高的10个词为：

顶部

	w	正数，指的是天
	Quantity[w,timeunit]	时长为 w ，单位为 timeunit
	Quantity[n,"Events"]	用事件计数 n 来定义窗口大小