MultivariateHypergeometricDistribution
MultivariateHypergeometricDistribution[n,{m1,m2,…,mk}]
i 型の mi個のオブジェクトを含む集合から n 回の非復元抽出を行う多変量超幾何分布を表す.
詳細
- 多項分布における非負の整数
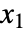 ,
, 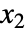 , …,
, …, 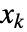 のベクトル
のベクトル 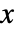 の確率は,
の確率は,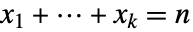 であるならば
であるならば ![product_(i=1)^kTemplateBox[{{m, _, i}, {x, _, i}}, Binomial] product_(i=1)^kTemplateBox[{{m, _, i}, {x, _, i}}, Binomial]](Files/MultivariateHypergeometricDistribution.ja/6.png) に比例する.
に比例する. - 数 miは任意の非負の整数でよく,n は m1+⋯+mk以下の任意の正の整数でよい.
- 試行回数 n は任意の正の整数でよく,miは任意の非負の整数でよい.
- MultivariateHypergeometricDistributionは,Mean,CDF,RandomVariate等の関数とともに使うことができる.
予備知識
- MultivariateHypergeometricDistribution[n,{m1,m2,…,mk}]は,
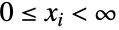 および
および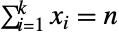 」を満足する整数のすべてのタプル
」を満足する整数のすべてのタプル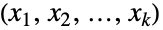 からなる
からなる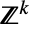 の部分集合上でサポートされ,各
の部分集合上でサポートされ,各 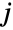 番目の(一変量)周辺分布が
番目の(一変量)周辺分布が 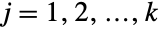 についてHypergeometricDistributionであるという特性で特徴付けられる多変量離散統計分布を表す.言葉を変えるなら,各変数
についてHypergeometricDistributionであるという特性で特徴付けられる多変量離散統計分布を表す.言葉を変えるなら,各変数 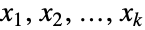 は
は 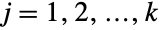 について xjHypergeometricDistribution[n,mj,m1+⋯+mk]を満足する.多変量超幾何分布は正の整数 n および非負の整数ベクトル{m1,m2,…,mk}によってパラメータ化される.これらは,ともに,分布の関連する平均,分散,共分散を定義する.
について xjHypergeometricDistribution[n,mj,m1+⋯+mk]を満足する.多変量超幾何分布は正の整数 n および非負の整数ベクトル{m1,m2,…,mk}によってパラメータ化される.これらは,ともに,分布の関連する平均,分散,共分散を定義する. - 多変量超幾何分布はタイプ i の mi個のオブジェクトを含む集合から置換えなしで n 回抽選する様子をモデル化する.これは,
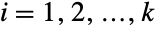 についてタイプ i のボールが mi個あるという条件下でタイプが異なる k 個のボールが入った壺から n 個のボールを抽出するモデルとして可視化することができる.多変量超幾何分布は,フランス人の数学者である1708年の論文中ではじめて分析された.この研究は,多変量超幾何分布に関する最初期のものとなっている.この分布は,不完全な検査手順を含むさまざまな現象の研究におけるツールとなっており,統計的決定理論等の分野のモデルとして広く利用されている.
についてタイプ i のボールが mi個あるという条件下でタイプが異なる k 個のボールが入った壺から n 個のボールを抽出するモデルとして可視化することができる.多変量超幾何分布は,フランス人の数学者である1708年の論文中ではじめて分析された.この研究は,多変量超幾何分布に関する最初期のものとなっている.この分布は,不完全な検査手順を含むさまざまな現象の研究におけるツールとなっており,統計的決定理論等の分野のモデルとして広く利用されている. - RandomVariateを使って,多変量超幾何分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,MultivariateHypergeometricDistribution[n,{m1,m2,…,mk}]] (より簡略な表記では xMultivariateHypergeometricDistribution[n,{m1,m2,…,mk}])を使って,確率変数 x が多変量超幾何分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[MultivariateHypergeometricDistribution[n,{m1,m2,…,mk}]]およびCDF[MultivariateHypergeometricDistribution[n,{m1,m2,…,mk}]]を使って得られる.平均,中央値,分散,共分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Covariance,Moment,CentralMomentを使って計算することができる.
- DistributionFitTestを使って,与えられたデータ集合が多変量超幾何分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータから多変量パラメトリック超幾何分布を推定することが,FindDistributionParametersを使ってデータを多変量超幾何分布にフィットすることができる.ProbabilityPlotを使って多変量記号超幾何分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って多変量記号超幾何分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換された多変量超幾何分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使って多変量超幾何分布を含む高次元分布を構築することが,ProductDistributionを使って多変量超幾何分布を含む独立成分分布の結合分布を計算することができる.
- MultivariateHypergeometricDistributionは,他の数多くの分布に関連している.この分布は,上述のように,HypergeometricDistributionと関係がある.MultivariateHypergeometricDistribution の一次元周辺確率密度関数は,それぞれHypergeometricDistributionであるが,多変量周辺分布は名前付きの分布に簡約することはできない.MultivariateHypergeometricDistributionの壺モデルは,後者は置き換えがある抽選モデルであるという意味で,MultinomialDistributionと関連がある.MultivariateHypergeometricDistributionは,一変量HypergeometricDistributionとの関係によって,GeometricDistribution,NormalDistribution,PoissonDistribution,PearsonDistribution,BetaBinomialDistributionとも関連がある.
例題
すべて開くすべて閉じるスコープ (7)
アプリケーション (1)
特性と関係 (2)
Wolfram Research (2010), MultivariateHypergeometricDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/MultivariateHypergeometricDistribution.html.
テキスト
Wolfram Research (2010), MultivariateHypergeometricDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/MultivariateHypergeometricDistribution.html.
CMS
Wolfram Language. 2010. "MultivariateHypergeometricDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MultivariateHypergeometricDistribution.html.
APA
Wolfram Language. (2010). MultivariateHypergeometricDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MultivariateHypergeometricDistribution.html