PearsonDistribution
✖
PearsonDistribution
✖
PearsonDistribution[a1,a0,b2,b1,b0]
represents a distribution of the Pearson family with parameters a1, a0, b2, b1, and b0.
Details
- The probability density
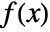satisfies the differential equation 
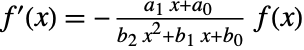. - The Pearson family of distributions is historically divided into seven types. By giving the form PearsonDistribution[type,…], the type will implicitly provide domain and parameter constraints.
- PearsonDistribution[1,…] is a shifted and rescaled BetaDistribution.
- PearsonDistribution[2,…] is a symmetric shifted and rescaled BetaDistribution.
- PearsonDistribution[3,…] includes NormalDistribution and GammaDistribution.
- PearsonDistribution[4,…] is not related to standard distributions.
- PearsonDistribution[5,…] is a shifted InverseGammaDistribution.
- PearsonDistribution[6,…] is a shifted and rescaled FRatioDistribution.
- PearsonDistribution[7,…] is a shifted and rescaled StudentTDistribution.
- With symbolic parameters and no type argument, the first type whose parameter assumptions are not explicitly violated is assumed. Types are tried in the order 4, 1, 6, 3, 5, 2, and 7.
- The parameter assumptions can be obtained from DistributionParameterAssumptions.
- PearsonDistribution allows a1, a0, b2, b1, and b0 to be quantities such that one can find a unit for x that makes
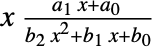dimensionless. » - PearsonDistribution can be used with such functions as Mean, CDF, and RandomVariate.
Background & Context
- PearsonDistribution represents a statistical distribution belonging to one of seven types as determined by argument structure. Pearson distributions originate with English mathematician Karl Pearson, who devised them in order to model distributions that are visibly skewed.
- The overall shape of the probability density function (PDF) of a Pearson distribution varies significantly based on its arguments. For example, the PDF of type I Pearson distributions may be either monotonic increasing, monotonic decreasing, or may have a single "peak" (i.e. a global maximum), whereas the PDF of type IV Pearson distributions always has a single peak and looks similar to skewed, asymmetric Gaussian distributions. In addition, the PDFs of various types of PearsonDistribution may be defined and supported over different types of intervals (for example, the domain of a type I Pearson is a bounded, finite-length interval, whereas the domain of a type IV is all of ), and the tails of the PDF may be "fat" (i.e. the PDF decreases non-exponentially for large values
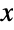) or "thin" (i.e. the PDF decreases exponentially for large 
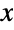), depending on the type. (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) - Pearson type IV is commonly used to fit distributions obtained from data or from Monte Carlo simulations, whereas the other Pearson families are intended to approximate unimodal distributions that are modeled well by type IV but not by other more "standard" distributions. Many distributions are described by (or are limiting values and/or special cases of) families of Pearson distributions, meaning Pearson distributions are extremely general in the types of phenomena they may model. For example, certain types of Pearson distributions play fundamental roles in describing disease transmission behavior, properties of Wiener processes, fundamental concepts in Bayesian statistics, the size of insurance claims, and bacterial gene expression.
- RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a Pearson distribution. Distributed[x,PearsonDistribution[type,a1,a0,b2,b1,b0]], written more concisely as xPearsonDistribution[type,a1,a0,b2,b1,b0], can be used to assert that a random variable x is distributed according to a Pearson distribution of a given type. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions for Pearson distributions of a given type may be given using PDF[PearsonDistribution[type,a1,a0,b2,b1,b0],x] and CDF[PearsonDistribution[type,a1,a0,b2,b1,b0],x]. Pearson distributions are special in the sense that their PDF satisfies a first-order differential equation involving a simple rational function of the form
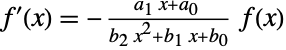. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively. When a Pearson distribution is finite, its first four moments uniquely determine it. - DistributionFitTest can be used to test if a given dataset is consistent with a Pearson distribution, EstimatedDistribution to estimate a Pearson parametric distribution from given data, and FindDistributionParameters to fit data to a Pearson distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic Pearson distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic Pearson distribution.
- TransformedDistribution can be used to represent a transformed Pearson distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a Pearson distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving Pearson distributions.
- PearsonDistribution is closely related to a number of other distributions. For example, types I and II Pearson distributions are shifted and rescaled versions of BetaDistribution, type III generalizes both NormalDistribution and GammaDistribution, type V is a shifted version of InverseGammaDistribution, and types VI and VII are shifted and rescaled versions of FRatioDistribution and StudentTDistribution, respectively. Though type IV Pearson distributions are unrelated to other standard distributions in this usual sense, they have PDFs that appear to be asymmetric versions of StudentTDistribution. Furthermore, for certain argument values, type IV Pearson distributions become generalizations of CauchyDistribution. PearsonDistribution is also closely related to ArcSinDistribution, BetaPrimeDistribution, PowerDistribution, ParetoDistribution, LevyDistribution, InverseChiSquareDistribution, HotellingTSquareDistribution, HalfNormalDistribution, and ErlangDistribution.
Examples
open allclose allBasic Examples (4)Summary of the most common use cases
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-b2fu6h
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-m9dff4
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-3vaj5h
Out[3]=3
Cumulative distribution function:
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-r723g
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-j6aki4
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-igky0d
Out[3]=3
Mean and variance of Pearson type 4:
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-flk83h
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-2yg9i
Out[2]=2
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-b3jhgq
Out[1]=1
Scope (8)Survey of the scope of standard use cases
Generate a sample of pseudorandom numbers from a Pearson distribution:
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-b7rt2v
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-fh95i
Out[2]=2
Distribution parameters estimation:
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-45b7g2
Estimate the distribution parameters from sample data:
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-epi747
Out[2]=2
Compare the density histogram of the sample with the PDF of the estimated distribution:
In[3]:=3
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-f8ui5o
Out[3]=3
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-lvfv01
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-54wnsr
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-ne54uk
Out[3]=3
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-tdfjid
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-0zlacd
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-bpy8e9
Out[3]=3
Different moments with closed forms as functions of parameters of Pearson type 4:
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-js043h
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-rx074o
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-d71a5p
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-pknsqa
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-6f3ti3
Out[5]=5
In[6]:=6
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-zg9ct4
Out[6]=6
In[7]:=7
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-9gzmth
Out[7]=7
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-45gate
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-rqy12o
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-pgdppw
Out[3]=3
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-joadzg
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-gqkhgo
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-z4fo9n
Out[3]=3
Consistent use of Quantity in parameters yields QuantityDistribution:
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-hmsba2
Out[1]=1
Find skewness of the option price under this model:
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-bo77b6
Out[2]=2
Applications (3)Sample problems that can be solved with this function
PearsonDistribution of type 4 is the only type not related to other standard distributions:
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-bl435p
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-d1f27
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-cb7o03
In[4]:=4
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-ga82zq
Out[4]=4
Find the probability for a Pearson IV random variate to be outside the plotted region:
In[5]:=5
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-h1jazq
Out[5]=5
Moments of PearsonDistribution satisfy a three-term recurrence equation implied by the defining differential equation for the density function 
:
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-bzb1sb
Express moment equations using standardized central moments:
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-b3bp73
Out[2]=2
Augment equations to fix coefficient normalization:
In[3]:=3
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-cjvcul
In[4]:=4
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-d1nx52
Out[4]=4
Define Pearson distribution in terms of standardized central moments:
In[5]:=5
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-b45n4
Out[5]=5
In[6]:=6
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-uzepc
Out[6]=6
In[7]:=7
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-kytsd9
Out[7]=7
In[8]:=8
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-cmzkt9
Out[8]=8
In[9]:=9
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-d348kk
Out[9]=9
Define Pearson distribution with zero mean and unit variance, and parameterized by skewness and kurtosis:
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-hshyga
Obtain parameter inequalities for Pearson types 1, 4, and 6:
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-46zj1
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-26mr9
In[4]:=4
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-hp3zyw
Determine the type of PearsonDistribution whose moments match sampling moments:
In[5]:=5
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-4eqpc
Out[5]=5
Compare with the estimated distribution:
In[6]:=6
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-qr39o
Out[6]=6
Properties & Relations (24)Properties of the function, and connections to other functions
Certain members of the PearsonDistribution family are closed under affine transforms:
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-etmnr
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-eqgrt2
Out[2]=2
Relationships to other distributions:
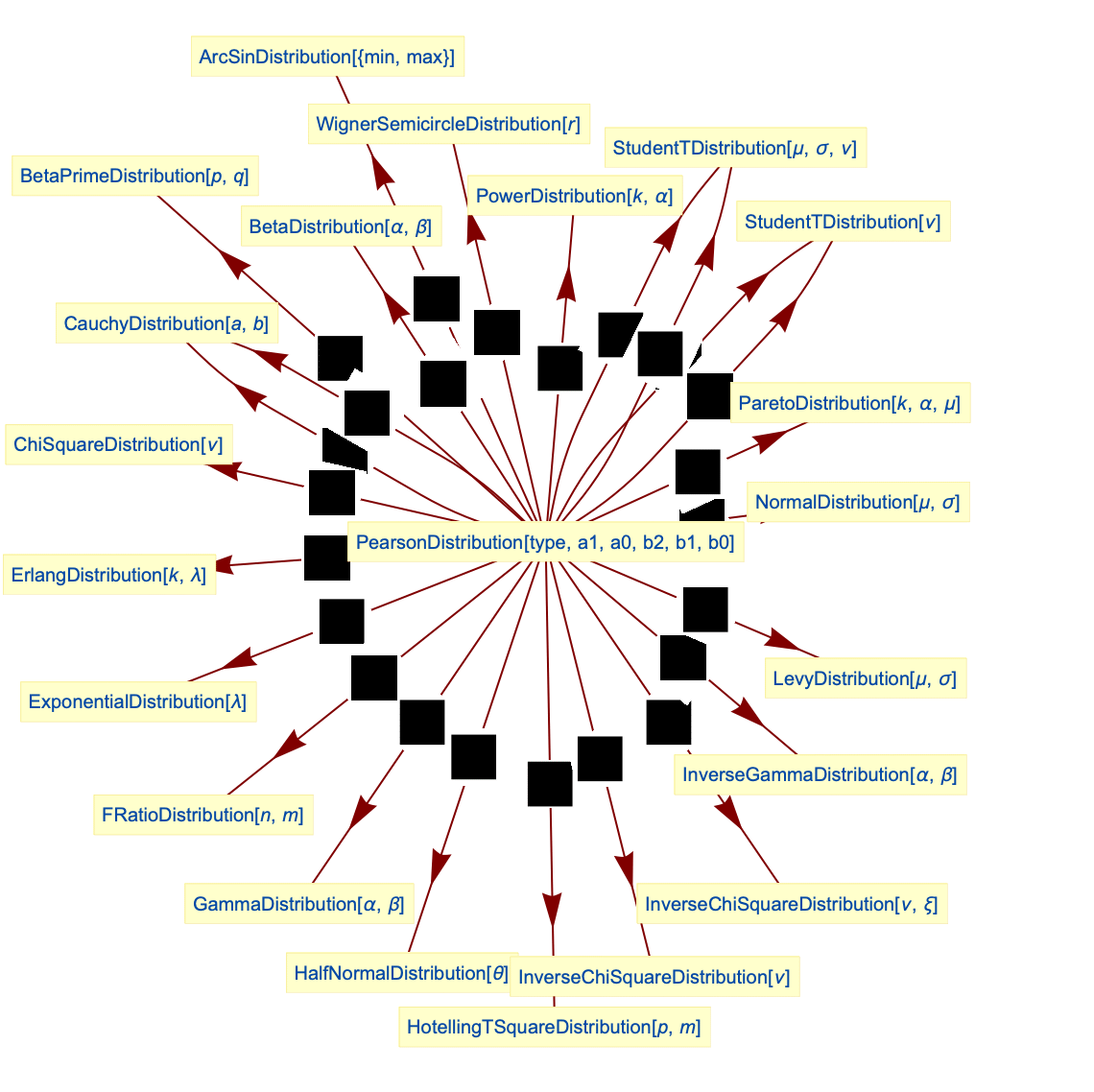
ArcSinDistribution is a special type of Pearson type 1 and type 2 distributions:
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-gd4fsp
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-3tja7u
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-vh9gg0
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-erhmc9
Out[4]=4
BetaDistribution is a special case of Pearson type 1 distribution:
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-x3yp0y
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-negofw
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-nktwja
Out[3]=3
PowerDistribution is a special case of Pearson type 1 distribution:
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-6ng28y
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-01h3pi
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-9itnye
Out[3]=3
WignerSemicircleDistribution is a special case of Pearson type 1 and type 2 distributions:
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-0y5as3
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-muqju3
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-smoa0u
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-ylwno8
Out[4]=4
ChiSquareDistribution is a special case of Pearson type 3 distribution:
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-2a1tgg
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-j3sph5
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-1ijdyq
Out[3]=3
ErlangDistribution is a special case of Pearson type 3 distribution:
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-4gzlwb
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-rikkdt
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-q1f88d
Out[3]=3
ExponentialDistribution is a special case of Pearson type 3 distribution:
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-q9ld0b
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-3cr68n
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-ost8vz
Out[3]=3
GammaDistribution is a special case of Pearson type 3 distribution:
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-yh1j16
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-bcxz8w
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-6o27vn
Out[3]=3
Scaled HalfNormalDistribution is a special case of Pearson type 3 distribution:
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-yknk7q
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-mtf1cd
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-4hw769
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-x6b3l1
Out[4]=4
NormalDistribution is a special case of Pearson type 3 distribution:
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-xnrrmj
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-j864on
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-dh0y64
Out[3]=3
CauchyDistribution is a limiting case of Pearson type 4 distribution:
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-lbuz5v
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-pk8b05
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-rr75s9
Out[3]=3
CauchyDistribution is a special case of Pearson type 7 distribution:
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-yioikr
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-k6ca4y
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-rguy6p
Out[3]=3
StudentTDistribution is a special case of Pearson type 4 and type 7 distributions:
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-nskf6v
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-qvx0i8
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-c9smn1
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-0981af
Out[4]=4
Generalized StudentTDistribution is a special case of Pearson type 4 and type 7 distributions:
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-cvm47m
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-mlp0za
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-6acro0
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-m5bmdb
Out[4]=4
InverseChiSquareDistribution is a special case of Pearson type 5 distribution:
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-uaqgc7
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-b457ad
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-yfws20
Out[3]=3
Scaled InverseChiSquareDistribution is a special case of Pearson type 5 distribution:
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-ovb393
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-o6um18
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-nobrgg
Out[3]=3
InverseGammaDistribution is a special case of Pearson type 5 distribution:
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-9hzd6o
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-84oc9z
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-ysgv6j
Out[3]=3
LevyDistribution is a special case of Pearson type 5 distribution:
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-3ue547
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-b2jca6
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-84pwjv
Out[3]=3
BetaPrimeDistribution is a special case of Pearson type 6 distribution:
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-wtirf0
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-6w21qe
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-m78srd
Out[3]=3
FRatioDistribution is a special case of Pearson type 6 distribution:
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-5blvj7
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-xyd3pk
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-wgyuig
Out[3]=3
HotellingTSquareDistribution is a special case of Pearson type 6 distribution:
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-skz0uo
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-exw3x3
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-whoxzk
Out[3]=3
ParetoDistribution is a special case of Pearson type 6 distribution:
In[1]:=1
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-prarfb
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-es1yyr
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0cf2cwmwrl3vkii-ylnd93
Out[3]=3
Wolfram Research (2010), PearsonDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/PearsonDistribution.html (updated 2016).
✖
Wolfram Research (2010), PearsonDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/PearsonDistribution.html (updated 2016).Text
Wolfram Research (2010), PearsonDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/PearsonDistribution.html (updated 2016).
✖
Wolfram Research (2010), PearsonDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/PearsonDistribution.html (updated 2016).CMS
Wolfram Language. 2010. "PearsonDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/PearsonDistribution.html.
✖
Wolfram Language. 2010. "PearsonDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/PearsonDistribution.html.APA
Wolfram Language. (2010). PearsonDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PearsonDistribution.html
✖
Wolfram Language. (2010). PearsonDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PearsonDistribution.htmlBibTeX
✖
@misc{reference.wolfram_2025_pearsondistribution, author="Wolfram Research", title="{PearsonDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/PearsonDistribution.html}", note=[Accessed: 10-July-2025
]}BibLaTeX
✖
@online{reference.wolfram_2025_pearsondistribution, organization={Wolfram Research}, title={PearsonDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/PearsonDistribution.html}, note=[Accessed: 10-July-2025
]}