NDEigenvalues[ℒ[u[x,y,…]],u,{x,y,…}∈Ω,n]
给出线性微分算子 ℒ 在区域 Ω 上 n 个最小量级的特征值.
NDEigenvalues[{ℒ1[u[x,y,…],v[x,y,…],…],ℒ2[u[x,y,…],v[x,y,…],…],…},{u,v,…},{x,y,…}∈Ω,n]
给出区域 Ω 上耦合微分算子 {op1,op2,…} 的特征值.
NDEigenvalues[eqns,{u,…},t,{x,y,…}∈Ω,n]
给出耦合时间相关微分方程 eqns 的解 u,… 空间变量 {x,y,…} 中的特征值.


NDEigenvalues
NDEigenvalues[ℒ[u[x,y,…]],u,{x,y,…}∈Ω,n]
给出线性微分算子 ℒ 在区域 Ω 上 n 个最小量级的特征值.
NDEigenvalues[{ℒ1[u[x,y,…],v[x,y,…],…],ℒ2[u[x,y,…],v[x,y,…],…],…},{u,v,…},{x,y,…}∈Ω,n]
给出区域 Ω 上耦合微分算子 {op1,op2,…} 的特征值.
NDEigenvalues[eqns,{u,…},t,{x,y,…}∈Ω,n]
给出耦合时间相关微分方程 eqns 的解 u,… 空间变量 {x,y,…} 中的特征值.
更多信息和选项

- NDEigenvalues,亦称为本征模求解器,是一个数值特征值求解器,用于求区域上微分方程的特征值.
- NDEigenvalues 给出 n 个最小量级特征值 λi 的列表 {λ1,…,λn}.
- 方程 eqns 与 NDSolve 中所指定的相同.
- 特征值按绝对值递增的顺序排序.
- 可以包括同质的 DirichletCondition、NeumannValue 或广义罗宾边界条件. »
- 可以包含 PeriodicBoundaryCondition .
- 如果没有对边界 ∂Ω 上的某些部分指定边界条件,则相当于指定 Neumann 0 边界条件.
- 对于一阶时间相关方程组的系统而言,时间导数 D[u[t,x,y,…],t],D[v[t,x,y,…],t],…, …. 实际上被 λ u[x,y,…],λ v[x,y,…],… 替代.
- 高于一阶的时间相关方程组系统被分解为含介值 ut=u*,
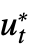 =..., vt=v*,
=..., vt=v*,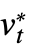 =... 的共轭一阶系统. 只返回函数 u、 v, … »
=... 的共轭一阶系统. 只返回函数 u、 v, … » - NDEigenvalues 接受 Method 可用于控制解的不同步骤的选项. 通过 Method->{s1->m1,s2->m2,…}, 步骤 si 由方法 mi 处理. 当步骤没有显式给出时, NDEigenvalues 尝试自动决定将给定方法应用于哪个步骤.
- 可能的求解步骤是:
-
"PDEDiscretization" 空间算子的离散化. "Eigensystem" 从离散系统中计算特征系统. "VectorNormalization" 被用于构建特征函数的特征向量的标准化.
范例
打开所有单元 关闭所有单元范围 (12)
一维 (7)
选项 (6)
Method (6)
"Eigensystem" (4)
求 Sturm–Liouville 算子在 ![]() 内的两个特征值,其中,Eigenvalues 使用 FEAST 方法:
内的两个特征值,其中,Eigenvalues 使用 FEAST 方法:
根据 Sturm–Liouville 理论,特征值必须是不同的,但在此例中,它们几乎简并:
区间的端点 ![]() 不包含在 FEAST 求特征值的区间中;如果想了解更多信息,请查阅 Eigenvalues 参考页面.
不包含在 FEAST 求特征值的区间中;如果想了解更多信息,请查阅 Eigenvalues 参考页面.
"PDEDiscretization" (1)
应用 (4)
声学 (1)
属性和关系 (3)
可能存在的问题 (10)
NDEigenvalue 将 PDE 转换为时间依赖的 PDE. 这种转换不是唯一的,并且可能导致耦合 PDE 出现意外的结果:
在内部,给定方程被重写为时间依赖的 PDE 方程组. 在上面的例子中,根据给定的因变量 {v[x],u[x]},生成以下含时方程组:{D[v[t, x], t] == - u[t, x] - Laplacian[u[t, x], {x}],D[u[t, x], t] == -v[t, x] - Laplacian[v[t, x], {x}]}
可在 Finite Element Method Usage Tips 中找到更多关于这个问题的讨论.
有些情况下,NDEigenvalues 可能会返回关于耦合 PDE 的出乎意料的结果:
避免此问题的一种方法是通过 "InterpolationOrder" 选项指定因变量的顺序:
可在 Finite Element Method Usage Tips 中找到更多关于这个问题的讨论.
NDEigenvalues 求给定线性微分算子的 ![]() 个最小量级特征值. 特别是在需要找到最负特征值的情况下,例如在许多量子力学问题中,
个最小量级特征值. 特别是在需要找到最负特征值的情况下,例如在许多量子力学问题中,![]() 个负值最大的特征值可能与 NDEigenvalues 默认返回的
个负值最大的特征值可能与 NDEigenvalues 默认返回的 ![]() 个特征值不一致. 要了解这一点,请看下面的范例.
个特征值不一致. 要了解这一点,请看下面的范例.
以氢原子的无量纲径向薛定谔方程为例,能量单位为雷德贝格(Rydbergs),长度以玻尔半径(Bohr radii)为单位.
这些特征值与最接近 ![]() 的特征值相对应. 比如,请查看以下问题的分析特征值.
的特征值相对应. 比如,请查看以下问题的分析特征值.
如果你事先知道特征值的下限,比如下标 ![]() ,你就可以将特征值问题
,你就可以将特征值问题 ![]() 重新定义为
重新定义为 ![]() . 换句话说,这是一个新的特征值问题:
. 换句话说,这是一个新的特征值问题:![]() ,其中
,其中 ![]() 且
且 ![]() . 鉴于
. 鉴于 ![]() 是
是 ![]() 的负下限,移位确保了
的负下限,移位确保了 ![]() 只能取正值. 因此,
只能取正值. 因此,![]() 的
的 ![]() 个量级最小值将对应于
个量级最小值将对应于 ![]() 的
的 ![]() 个负值最大的值. 这样,我们就可以计算出
个负值最大的值. 这样,我们就可以计算出 ![]() ,然后得到
,然后得到 ![]() . 最简单的方法是使用 "Shift" 选项.
. 最简单的方法是使用 "Shift" 选项.
这些特征值与负值最大的特征值相对应,但顺序相反,因此有必要对特征状态进行排序.
使用 Sort 对特征状态进行排序:
技术笔记
文本
Wolfram Research (2015),NDEigenvalues,Wolfram 语言函数,https://reference.wolfram.com/language/ref/NDEigenvalues.html.
CMS
Wolfram 语言. 2015. "NDEigenvalues." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/NDEigenvalues.html.
APA
Wolfram 语言. (2015). NDEigenvalues. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/NDEigenvalues.html 年
BibTeX
@misc{reference.wolfram_2025_ndeigenvalues, author="Wolfram Research", title="{NDEigenvalues}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/NDEigenvalues.html}", note=[Accessed: 15-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_ndeigenvalues, organization={Wolfram Research}, title={NDEigenvalues}, year={2015}, url={https://reference.wolfram.com/language/ref/NDEigenvalues.html}, note=[Accessed: 15-January-2026]}