NegativeMultinomialDistribution
NegativeMultinomialDistribution[n,p]
母数 n,失敗確率ベクトル p の負の多項分布を表す.
詳細

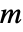 が負の多項分布において
が負の多項分布において 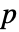 の長さである非負の整数
の長さである非負の整数 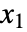 ,
, 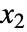 , …,
, …, 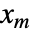 のベクトル
のベクトル 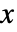 の確率は,
の確率は,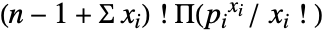 に比例する.
に比例する.- 母数 n は任意の正の実数でよく,p は総和が1より小さい非負の実数の任意のベクトルでよい.
- n が正の整数の場合,NegativeMultinomialDistribution[n,p]は成功確率1-Total[p],n 回成功するまでの失敗がLength[p]通りとして試行を続けた場合の失敗数の分布を与える.
- NegativeMultinomialDistributionでは,n とベクトル p の成分は無次元量でよい. »
- NegativeMultinomialDistributionは,Mean,CDF,RandomVariate等の関数とともに使うことができる.
予備知識
- NegativeMultinomialDistribution[n,{p1,p2,…,pm}]は,
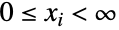 を満足する整数すべてのタプル
を満足する整数すべてのタプル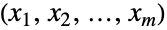 からなる
からなる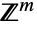 の部分集合上でサポートされ,
の部分集合上でサポートされ,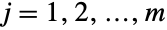 のとき,
のとき, 番目の(一変量)周辺分布のそれぞれがNegativeBinomialDistributionであるという特性によって特徴付けられた多変量離散統計分布を表す.他の言葉で表現するなら,
番目の(一変量)周辺分布のそれぞれがNegativeBinomialDistributionであるという特性によって特徴付けられた多変量離散統計分布を表す.他の言葉で表現するなら,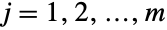 のとき,各変数
のとき,各変数 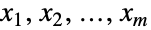 はある確率 qjについて xjBinomialDistribution[n,qj]を満足する.負の多項分布は正の実数 n および
はある確率 qjについて xjBinomialDistribution[n,qj]を満足する.負の多項分布は正の実数 n および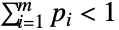 を満足する非負の実数からなるベクトル{p1,p2,…,pm}(「失敗確率ベクトル」と呼ばれる)によってパラメータ化される.これらは,ともに,分布に関連付けられた平均,分散,共分散を定義する.
を満足する非負の実数からなるベクトル{p1,p2,…,pm}(「失敗確率ベクトル」と呼ばれる)によってパラメータ化される.これらは,ともに,分布に関連付けられた平均,分散,共分散を定義する. - 負の多項分布は,負の一変量二項分布(NegativeBinomialDistribution)の変形として1950年代の中頃にはじめて調べられた.一変量の場合と同じように,整数 n についてのNegativeMultinomialDistribution[n,{p1,p2,…,pm}]は,成功確率が
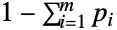 で n 回の成功までの失敗に m 個のタイプがある一連の試行における失敗数の分布を与える.負の多項分布は流行病,事故の頻度,信頼性,職場の欠勤等を含む現象のモデル化に使われている.
で n 回の成功までの失敗に m 個のタイプがある一連の試行における失敗数の分布を与える.負の多項分布は流行病,事故の頻度,信頼性,職場の欠勤等を含む現象のモデル化に使われている. - RandomVariateを使って,負の多項分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,NegativeMultinomialDistribution[n,{p1,p2,…,pm}]]より簡略な表記では xNegativeMultinomialDistribution[n,{p1,p2,…,pm}])を使って,確率変数 x が負の多項分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[NegativeMultinomialDistribution[n,{p1,p2,…,pm}]]およびCDF[NegativeMultinomialDistribution[n,{p1,p2,…,pm}]]を使って得られる.平均,中央値,分散,共分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Covariance,Moment,CentralMomentを使って計算することができる.
- DistributionFitTestを使って,与えられたデータ集合が負の多項分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータから負のパラメトリック多項分布を推定することが,FindDistributionParametersを使ってデータを負の多項分布にフィットすることができる.ProbabilityPlotを使って負の記号多項分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って負の記号多項分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換された負の多項分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使って負の多項分布を含む高次元分布を構築することが,ProductDistributionを使って負の多項分布を含む独立成分分布の結合分布を計算することができる.
- NegativeMultinomialDistributionは他の多の分布と関連している.この分布は,NegativeBinomialDistribution[n,p]の変数 x についての確率密度関数が{x}ベクトについて書かれたNegativeMultinomialDistribution[n,{1-p}]のそれと厳密に等しいという意味で,NegativeBinomialDistributionの高次一般化である.NegativeMultinomialDistributionは,BinomialDistribution,MultinomialDistribution.BernoulliDistribution,BetaBinomialDistribution,HypergeometricDistribution,GeometricDistribution,PoissonDistributionとも関係がある.
例題
すべて開くすべて閉じるスコープ (9)
位一変量周辺分布はNegativeBinomialDistributionを与える:
多変量周辺分布はNegativeMultinomialDistributionを与える:
無次元のQuantityを使ってNegativeMultinomialDistributionを定義する:
アプリケーション (1)
考えられる問題 (3)
n が正の整数でなければ,NegativeMultinomialDistributionは定義されない:
p が1より小さい総和となる確率のベクトルでなければ,NegativeMultinomialDistributionは定義されない:
テキスト
Wolfram Research (2010), NegativeMultinomialDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/NegativeMultinomialDistribution.html (2016年に更新).
CMS
Wolfram Language. 2010. "NegativeMultinomialDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/NegativeMultinomialDistribution.html.
APA
Wolfram Language. (2010). NegativeMultinomialDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NegativeMultinomialDistribution.html