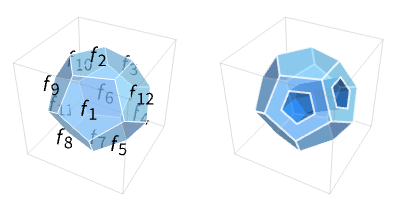
Polyhedron[{f1,…,fn}]
represents a filled polyhedron inside the closed surfaces with polygon faces fi.
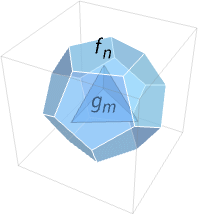
Polyhedron[{f1,…,fn}{{g1,…,gm},…}]
represents a polyhedron with voids {g1,…,gm},….
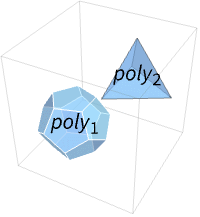
Polyhedron[{poly1,poly2,…}]
represents a collection of polyhedra polyi.
Polyhedron[{p1,…,pn},data]
represents a polyhedron in which coordinates given as integers i in data are taken to be pi.


Polyhedron
Polyhedron[{f1,…,fn}]
represents a filled polyhedron inside the closed surfaces with polygon faces fi.
Polyhedron[{f1,…,fn}{{g1,…,gm},…}]
represents a polyhedron with voids {g1,…,gm},….
Polyhedron[{poly1,poly2,…}]
represents a collection of polyhedra polyi.
Polyhedron[{p1,…,pn},data]
represents a polyhedron in which coordinates given as integers i in data are taken to be pi.
Details and Options



- Polyhedron can be used a geometric region and a graphics primitive.
- Polyhedron[{f1,…,fn}] is a volume region, representing all the points inside the closed surface with polygon faces fi.
- A point is an element of the polyhedron if a ray from the point in any direction crosses the boundary polygon faces an odd number of times.
- Polyhedron[{f1,…,fn}{{g1,…,gm},…}] specifies a polyhedron with voids consisting of an outer polyhedron Polyhedron[{f1,…,fn}] and one or several inner polyhedra Polyhedron[{g1,…,gm}],….
- A point p is an element of the polyhedron if it is in the outer polyhedron but not in any inner polyhedron.
- Polyhedron[{poly1,poly2,…}] is a collection of polyhedra polyi with or without voids and is treated as a union of polyi for geometric computations.
- Polyhedron[{p1,…,pn},data] effectively replaces integers i that appear as coordinates in data by the corresponding pi.
-
Polyhedron[{p1,…,pn},{f1,…,fn}] polyhedron boundary faces fi with points {po1,…,pok} Polyhedron[{p1,…,pn},{{f1,…,fk}{{g1,…,gl},…}] outer polyhedron boundary faces fi with points {po1,…,pok} and inner polyhedron boundary faces gj with points {pv1,…,pvl} etc. Polyhedron[{p1,…,pn},{{b1,…,bn},{f1,…,fk}{{g1,…,gl},…},…}] a collection of several polyhedra - As a geometric region, the polygon faces fi can have any embedding dimension, but must all be simple polygons and have the same embedding dimension.
- In a graphics, the points of the polygon faces fi can be Scaled and Dynamic expressions.
- Graphics renderings is affected by directives such as FaceForm, EdgeForm, Texture, Specularity, Opacity and color.
- The following options and settings can be used in graphics:
-
VertexColors Automatic vertex colors to be interpolated VertexNormals Automatic effective vertex normals for shading VertexTextureCoordinates None coordinates for textures
Examples
open all close allScope (11)
Graphics (8)
Styling (5)
Color directives specify the face colors of polyhedra:
Texture can be used to specify a texture to be used on the faces of polyhedra:
Texture can work together with a different Opacity:
Texture can work together with different Lighting:
FaceForm and EdgeForm can be used to specify the styles of the edges and faces:
Colors can be specified at vertices using VertexColors:
Normals can be specified at vertices using VertexNormals for polyhedra:
Coordinates (1)
Use Scaled coordinates:
See Also
PolyhedronCoordinates OuterPolyhedron InnerPolyhedron Cube Dodecahedron Icosahedron Octahedron Tetrahedron Cuboid Hexahedron Parallelepiped Prism Pyramid Simplex PolyhedronData CanonicalizePolyhedron RandomPolyhedron MeshRegion
Function Repository: PolyhedronCanonicalForm OutlinePolygons PolyhedronChop
Related Guides
History
Text
Wolfram Research (2019), Polyhedron, Wolfram Language function, https://reference.wolfram.com/language/ref/Polyhedron.html.
CMS
Wolfram Language. 2019. "Polyhedron." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Polyhedron.html.
APA
Wolfram Language. (2019). Polyhedron. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Polyhedron.html
BibTeX
@misc{reference.wolfram_2025_polyhedron, author="Wolfram Research", title="{Polyhedron}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/Polyhedron.html}", note=[Accessed: 02-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_polyhedron, organization={Wolfram Research}, title={Polyhedron}, year={2019}, url={https://reference.wolfram.com/language/ref/Polyhedron.html}, note=[Accessed: 02-January-2026]}