represents a regular octahedron centered at the origin with unit edge length.
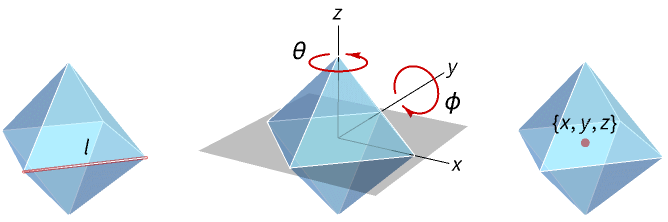
Octahedron[l]
represents an octahedron with edge length l.
Octahedron[{θ,ϕ},…]
represents an octahedron rotated by an angle θ with respect to the z axis and angle ϕ with respect to the y axis.
Octahedron[{x,y,z},…]
represents an octahedron centered at {x,y,z}.


Octahedron
represents a regular octahedron centered at the origin with unit edge length.
Octahedron[l]
represents an octahedron with edge length l.
Octahedron[{θ,ϕ},…]
represents an octahedron rotated by an angle θ with respect to the z axis and angle ϕ with respect to the y axis.
Octahedron[{x,y,z},…]
represents an octahedron centered at {x,y,z}.
Details and Options

- Octahedron is also known as regular octahedron.
- Octahedron can be used as a geometric region and graphics primitive.
- Octahedron[] is equivalent to Octahedron[{0,0,0},1].
- Octahedron[l] is equivalent to Octahedron[{0,0,0},l].
- CanonicalizePolyhedron can be used to convert a octahedron to an explicit Polyhedron object.
- Octahedron can be used in Graphics3D.
- In graphics, the points and edge lengths can be Scaled and Dynamic expressions.
- Graphics rendering is affected by directives such as FaceForm, EdgeForm, Opacity, Texture and color.
- The following options and settings can be used in graphics:
-
VertexColors Automatic vertex colors to be interpolated VertexNormals Automatic effective vertex normals for shading VertexTextureCoordinates None coordinates for textures
Examples
open all close allScope (6)
Graphics (4)
Styling (3)
FaceForm and EdgeForm can be used to specify the styles of the faces and edges:
Apply a Texture to the faces:
Assign VertexColors to vertices:
Related Guides
History
Text
Wolfram Research (2019), Octahedron, Wolfram Language function, https://reference.wolfram.com/language/ref/Octahedron.html.
CMS
Wolfram Language. 2019. "Octahedron." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Octahedron.html.
APA
Wolfram Language. (2019). Octahedron. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Octahedron.html
BibTeX
@misc{reference.wolfram_2025_octahedron, author="Wolfram Research", title="{Octahedron}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/Octahedron.html}", note=[Accessed: 24-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_octahedron, organization={Wolfram Research}, title={Octahedron}, year={2019}, url={https://reference.wolfram.com/language/ref/Octahedron.html}, note=[Accessed: 24-January-2026]}