PowerSymmetricPolynomial
表示具有指数 r 的形式幂对称多项式.
PowerSymmetricPolynomial[{r1,r2,…}]
表示指数为 r1、r2、… 的多元形式幂对称多项式.
PowerSymmetricPolynomial[rspec,data]
给出 data 中的幂对称多项式.
更多信息
- PowerSymmetricPolynomial[r,{x1,x2,…,xn}] 由
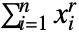 给出.
给出. - PowerSymmetricPolynomial[{r1,r2,…},{{x11,x12,…},…,{xn 1,xn 2,…}}] 由
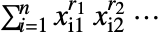 给出.
给出. - PowerSymmetricPolynomial[rspec] 可以用以表示用于矩估计的形式幂和式.
- MomentConvert 可以用来以 PowerSymmetricPolynomial 对象的形式产生矩估计量.
- MomentEvaluate 可以用以计算数据集上的形式 PowerSymmetricPolynomial 对象的多项式.
范例
打开所有单元关闭所有单元基本范例 (1)
范围 (3)
应用 (1)
使用 AugmentedSymmetricPolynomial 将幂对称多项式线性化:
属性和关系 (1)
Wolfram Research (2010),PowerSymmetricPolynomial,Wolfram 语言函数,https://reference.wolfram.com/language/ref/PowerSymmetricPolynomial.html.
文本
Wolfram Research (2010),PowerSymmetricPolynomial,Wolfram 语言函数,https://reference.wolfram.com/language/ref/PowerSymmetricPolynomial.html.
CMS
Wolfram 语言. 2010. "PowerSymmetricPolynomial." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/PowerSymmetricPolynomial.html.
APA
Wolfram 语言. (2010). PowerSymmetricPolynomial. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/PowerSymmetricPolynomial.html 年