Projection
Projection[u,v]
ベクトル u をベクトル v へ射影したものを返す.
Projection[u,v,f]
内積関数 f についての射影を返す.
詳細
- 通常の実数ベクトル u および v については,射影は
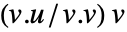 であると考えられる.
であると考えられる. - 通常の複素ベクトル u および v については,射影は
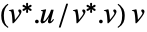 であると考えられる.ただし,
であると考えられる.ただし,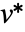 はConjugate[v]である. »
はConjugate[v]である. » - Projection[u,v,f]の場合,u と v は,内積関数 f がペアに適用された場合に実数の結果を返すような任意の式または式のリストでよい. »
- Projection[u,v,Dot]は,事実上,u と v のすべての要素が実数であると仮定する. »
例題
すべて開くすべて閉じるスコープ (9)
基本的な用法 (9)
すべての式が実数値であると仮定してDotの内積を与える:
アプリケーション (18)
幾何 (4)
Projectionを使って,ベクトル ![]() に直角な線についてのベクトル
に直角な線についてのベクトル ![]() の反射を得る:
の反射を得る:
Since ![]() は直線に直角なので,
は直線に直角なので,![]() の2倍を引くと線について
の2倍を引くと線について ![]() が反射される:
が反射される:
ReflectionTransformの結果と比較する:
![]() とその反射を
とその反射を ![]() によって2回繰り返される平行移動として可視化する:
によって2回繰り返される平行移動として可視化する:
フレネ・セレ(Frenet–Serret)の系はすべての空間曲線の特性をベクトル基底およびスカラー関数で符号化する.次の曲線(螺旋)について考える:
平行射影を引くことで最初の3つの導関数から正規直交基底を構築する:
FrenetSerretSystemを使って答を確かめる:
基底分解と行列分解 (3)
グラム・シュミット(Gram–Schmid)過程を適用して次のベクトルから正規直交基底を構築する:
正規直交規定 ![]() の最初のベクトルは,単に正規化された複数の
の最初のベクトルは,単に正規化された複数の ![]() に過ぎない:
に過ぎない:
続くベクトルについては,前の基底ベクトルの平行の成分は正規化の前に引かれる:
Orthogonalizeを使って答を確認する:
次の行列 ![]() の列空間についての正規直交基底を求め,その基底を使って
の列空間についての正規直交基底を求め,その基底を使って ![]() のQR分解を求める:
のQR分解を求める:
![]() を対応するグラム・シュミット基底の
を対応するグラム・シュミット基底の ![]() 番目の要素として定義する:
番目の要素として定義する:
QRDecompositionの結果と比較する.![]() 行列は等しい:
行列は等しい:
QRDecompositionは行正規直交の結果を与えるので,![]() 行列は転置分だけ異なる:
行列は転置分だけ異なる:
エルミート(Hermite)行列(より一般的には任意の正規行列)の固有ベクトルは直交ベクトルであり,射影行列は ![]() と定義するのが一般的である.ただし,
と定義するのが一般的である.ただし,![]() は正規化された固有ベクトルである.一般ベクトル上への射影行列の動作が次の行列
は正規化された固有ベクトルである.一般ベクトル上への射影行列の動作が次の行列 ![]() について固有空間へのベクトルの射影と等しいことを示す:
について固有空間へのベクトルの射影と等しいことを示す:
一般ベクトルを ![]() 倍することは
倍することは ![]() へのベクトルの射影に等しいことを確認する:
へのベクトルの射影に等しいことを確認する:
最小二乗と曲線のフィット (3)
線形系 ![]() に解がない場合,最良の近似解は最小二乗解である.それは
に解がない場合,最良の近似解は最小二乗解である.それは ![]() の解である.ただし,
の解である.ただし,![]() は
は ![]() の列空間への
の列空間への ![]() の直交射影である.次の
の直交射影である.次の ![]() と
と ![]() について考える:
について考える:
![]() をスパンする直交ベクトルを求める.まず,
をスパンする直交ベクトルを求める.まず,![]() は
は ![]() の第1列であるとする:
の第1列であるとする:
LeastSquaresを使って結果を確かめる:
Projectionを使ってデータに最もフィットする曲線が求められる.次のデータについて考える:
![]() を最小化することが線
を最小化することが線 ![]() にフィットすることになるように
にフィットすることになるように![]() が列
が列 ![]() と
と ![]() を持つとする:
を持つとする:
次の2つの直交ベクトルは明らかに ![]() の列と同じ空間をスパンしている:
の列と同じ空間をスパンしている:
Fitを使って係数を確かめる:
![]() を最小にすることが
を最小にすることが ![]() にフィットすることになるように,
にフィットすることになるように,![]() が列
が列 ![]() ,
,![]() ,
,![]() を持つとする:
を持つとする:
Fitを使って係数を確認する:
一般内積と関数空間 (5)
正定値実対称行列あるいは測定値 ![]() は
は![]() によって内積を定義する:
によって内積を定義する:
正定値であるということは,関連する二次形式 ![]() が
が ![]() のときは正であることを意味する:
のときは正であることを意味する:
Dotそれ自体が恒等行列に関連付けられた内積である点に注意のこと:
グラム・シュミット過程を標準基底に適用して正規直交基底を得る:
フーリエ級数は内積空間 ![]() 内の特定の基底への射影である.自乗可積分関数で標準の内積を定義する:
内の特定の基底への射影である.自乗可積分関数で標準の内積を定義する:
関数 ![]() のフーリエ級数は
のフーリエ級数は ![]() によってスパンされた空間への
によってスパンされた空間への ![]() の射影である:
の射影である:
FourierSeriesを使って結果を確かめる:
さらに,![]() はFourierParameters{-1,1}に対応するフーリエ級数に等しい:
はFourierParameters{-1,1}に対応するフーリエ級数に等しい:
FourierCoefficientを使って確かめる:
3つのベクトルのランダムなセットにグラム・シュミットを行う:
直交性を確認する.ベクトルが正規化されていないので,結果は一般的な直交行列である:
グラム・シュミットを3つの複素ベクトルのランダム集合に対して行う:
LegendrePは直交多項式族を内積![]() について定義する.正規化されていないグラム・シュミット過程を単項式
について定義する.正規化されていないグラム・シュミット過程を単項式 ![]() (
(![]() は0から4まで)に適用して最初の5つのルジャンドル(Legendre)多項式のスカラー倍を計算する:
は0から4まで)に適用して最初の5つのルジャンドル(Legendre)多項式のスカラー倍を計算する:
各 ![]() について,
について,![]() と
と ![]() は定数倍数分だけ異なるが,これは
は定数倍数分だけ異なるが,これは![]() はに等しいことが分かる:
はに等しいことが分かる:
HermiteHは直交多項式族を内積![]() について定義する.正規化されていないグラム・シュミット過程を単項式
について定義する.正規化されていないグラム・シュミット過程を単項式 ![]() (
(![]() は0から4まで)に適用して最初の4つのエルミート多項式のスカラー倍を計算する:
は0から4まで)に適用して最初の4つのエルミート多項式のスカラー倍を計算する:
量子力学 (3)
量子力学では,状態は複素単位ベクトルで表され,物理量はエルミート線形演算子で表される. 固有値は可能な観測値を,固有ベクトルへの射影の2乗ノルムはそれらの観測値の確率を表す.与えられたスピン演算子 ![]() と状態
と状態 ![]() について,可能な観測値とその確率を求める:
について,可能な観測値とその確率を求める:
量子力学では,エネルギー演算子はハミルトニアン ![]() と呼ばれ,エネルギー
と呼ばれ,エネルギー ![]() の状態はシュレディンガー方程式
の状態はシュレディンガー方程式 ![]() に従って進化する.
に従って進化する.![]() 方向の一定磁場内のスピン1粒子のハミルトニアンが与えられたとして最初は
方向の一定磁場内のスピン1粒子のハミルトニアンが与えられたとして最初は ![]() を表す状態
を表す状態![]() にあった粒子の時点
にあった粒子の時点 ![]() におけるの状態を求める:
におけるの状態を求める:
時点 ![]() における状態はシュレディンガー方程式に従って進化した各固有状態の和である:
における状態はシュレディンガー方程式に従って進化した各固有状態の和である:
ハミルトニアン ![]() について,
について,![]() 番目の固有ベクトルは
番目の固有ベクトルは ![]() の定数倍数で,ベクトルの内積は
の定数倍数で,ベクトルの内積は![]() である. 状態
である. 状態 ![]() の粒子が最初の4つの固有状態の1つにある確率を求める.まず,内積を定義する:
の粒子が最初の4つの固有状態の1つにある確率を求める.まず,内積を定義する:
特性と関係 (8)
![]() と
と ![]() が実数項を持つなら
が実数項を持つなら![]() である.ただし,
である.ただし, ![]() は
は ![]() と
と ![]() の間の角度である:
の間の角度である:
ベクトル u と v について u-Projection[u,v]は v と直交する:
OrthogonalizeはProjectionとNormalizeを繰り返し適用することで実装できる:
テキスト
Wolfram Research (2007), Projection, Wolfram言語関数, https://reference.wolfram.com/language/ref/Projection.html (2014年に更新).
CMS
Wolfram Language. 2007. "Projection." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/Projection.html.
APA
Wolfram Language. (2007). Projection. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Projection.html