Projection
Projection[u,v]
求向量 u 在向量 v 上的射影.
Projection[u,v,f]
求关于内积函数 f 的射影.
更多信息
- 对于原始实数向量 u 和 v,射影是
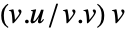 .
. - 对于原始复数向量 u 和 v,射影是
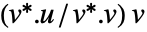 ,其中
,其中 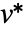 是 Conjugate[v].
是 Conjugate[v]. - 在 Projection[u,v,f] 中, u 和 v 可以是任何表达式或者表达式的列表,由内积函数 f 给出这些表达式的成对实结果. »
- Projection[u,v,Dot] 实际上假定 u 和 v 的所有元素都是实数. »
范例
打开所有单元关闭所有单元范围 (9)
Basic Uses (6)
General Inner Products (3)
应用 (18)
几何学 (4)
使用 Projection 将向量 ![]() 映射到向量
映射到向量 ![]() 的法线上:
的法线上:
由于 ![]() 垂直于直线,所以减去
垂直于直线,所以减去 ![]() 的两倍,就能将
的两倍,就能将 ![]() 映射到直线的另一侧:
映射到直线的另一侧:
与 ReflectionTransform 的结果进行比较:
Frenet–Serret 系统用向量基和标量函数对每条空间曲线的属性进行编码. 请见下面这条曲线(螺旋线):
使用 FrenetSerretSystem 验证答案:
基和矩阵分解 (3)
应用 Gram–Schmidt 过程并根据以下向量构造一个标准正交基:
使用 Orthogonalize 对结果进行验证:
找到以下矩阵 ![]() 的列空间的正交基,然后使用该基找到
的列空间的正交基,然后使用该基找到 ![]() 的 QR 分解:
的 QR 分解:
与 QRDecomposition 给出的结果进行比较;![]() 矩阵是相同的:
矩阵是相同的:
![]() 矩阵因转置而不同,因为 QRDecomposition 给出了行正交结果:
矩阵因转置而不同,因为 QRDecomposition 给出了行正交结果:
对于埃尔米特矩阵(可推广到任何正规矩阵),特征向量是正交的,并且通常定义投影矩阵 ![]() ,其中
,其中 ![]() 是正规化的特征向量. 证明投影矩阵对一般向量的作用与将向量投影到以下矩阵
是正规化的特征向量. 证明投影矩阵对一般向量的作用与将向量投影到以下矩阵 ![]() 的特征空间上的作用相同:
的特征空间上的作用相同:
最小二乘和曲线拟合 (3)
如果线性方程组 ![]() 没有解,则最好的近似解是最小二乘解. 这是
没有解,则最好的近似解是最小二乘解. 这是 ![]() 的解,其中
的解,其中 ![]() 是
是 ![]() 在
在 ![]() 的列空间上的正交投影. 思考以下
的列空间上的正交投影. 思考以下 ![]() 和
和 ![]() :
:
使用 LeastSquares 确认结果:
Projection 可用于找到数据的最佳拟合曲线. 思考以下数据:
使用 Fit 验证系数:
使用 Fit 验证系数:
一般内积和函数空间 (5)
请注意,Dot 本身是与单位矩阵相关的内积:
将 Gram–Schmidt 过程应用于标准基可获得正交基:
傅里叶级数是在内积空间 ![]() 中特定基上的投影. 定义平方可积函数的标准内积:
中特定基上的投影. 定义平方可积函数的标准内积:
使用 FourierSeries 验证结果:
而且,![]() 等于对应 FourierParameters{-1,1} 的傅里叶系数:
等于对应 FourierParameters{-1,1} 的傅里叶系数:
使用 FourierCoefficient 进行验证:
在 3 个向量的随机集合上进行 Gram–Schmidt 运算:
对三个复向量的随机集合进行 Gram–Schmidt 运算:
LegendreP 定义了关于内积 ![]() 的正交多项式族. 对
的正交多项式族. 对 ![]() 从 0 到 4 的单项式
从 0 到 4 的单项式 ![]() 应用非规范化的 Gram–Schmidt 过程,计算前五个勒让德多项式的标量倍数:
应用非规范化的 Gram–Schmidt 过程,计算前五个勒让德多项式的标量倍数:
对于每一个 ![]() ,
,![]() 和
和 ![]() 相差一个常数倍数,可以证明等于该倍数
相差一个常数倍数,可以证明等于该倍数 ![]() :
:
HermiteH 定义了关于内积 ![]() 的正交多项式族. 对
的正交多项式族. 对 ![]() 从 0 到 4 的单项式
从 0 到 4 的单项式 ![]() 应用非规范化的 Gram–Schmidt 过程,计算前四个埃尔米特多项式的标量倍数:
应用非规范化的 Gram–Schmidt 过程,计算前四个埃尔米特多项式的标量倍数:
属性和关系 (8)
对于向量 u 和 v,u-Projection[u,v] 与 v 正交:
Orthogonalize 可以通过重复应用 Projection 和 Normalize 来实现:
文本
Wolfram Research (2007),Projection,Wolfram 语言函数,https://reference.wolfram.com/language/ref/Projection.html (更新于 2014 年).
CMS
Wolfram 语言. 2007. "Projection." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2014. https://reference.wolfram.com/language/ref/Projection.html.
APA
Wolfram 语言. (2007). Projection. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Projection.html 年