Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

QnDispersion

QnDispersion[list]

gives the statistic of the elements in list.

QnDispersion[list,c]

gives the statistic with a scaling factor c.

Details and Options

QnDispersion is a robust measure of dispersion.
QnDispersion is a rank-based estimator with its statistic based on absolute pairwise differences. The statistic does not require location estimation.
For the list {x₁,x₂,…,x_n}, the value of the 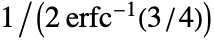statistic is given by the first quartile of the set {x_i– x_j,i<j} multiplied by a scaling factor c.
When c is not specified, a scaling factor 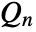is applied to make the 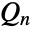statistic a consistent estimator of the scale parameter for normally distributed data. Also, a finite sample correction is used by default to make the estimator unbiased for small samples.
QnDispersion[{{x₁,y₁,…},{x₂,y₂,…},…}] gives {QnDispersion[{x₁,x₂,…}],QnDispersion[{y₁,y₂,…}],…}.
QnDispersion supports a Method option. The following explicit settings can be specified:
"FiniteSample" uses finite sample correction (default)

"None" no correction
The option Method is ignored if the scaling factor c is specified in the input.

Examples

open allclose all

Basic Examples (4)

QnDispersion of a list:

QnDispersion of columns of a matrix:

QnDispersion of a list with scaling factor 1:

QnDispersion of a list of dates:

Scope (8)

Exact input yields exact output when the scaling factor is exact:

QnDispersion with different scaling parameters:

QnDispersion for a matrix gives a columnwise estimate:

QnDispersion of a large array:

Find a QnDispersion of a TimeSeries:

The dispersion depends only on the values:

QnDispersion works with data involving quantities:

Compute QnDispersion of dates:

Compute QnDispersion of times:

List of times with different time zone specifications:

Options (1)

Method (1)

Finite sample correction is applied as default:

Without small sample correction:

Applications (6)

Obtain a robust estimate of dispersion when extreme values are present:

Sample standard deviation is heavily influenced by extreme values:

Identify periods of high volatility in stock data using a five-year moving dispersion:

Compute dispersion for slices of a collection of paths of a random process:

Choose a few slice times:

Plot dispersion over these paths:

Find the dispersion of the heights for the children in a class:

Plot the dispersion with respect to the median:

Consider data from standard normal distribution with outliers modeled by another normal distribution with large spread:

Test the data against standard normal distribution:

Compute the dispersion:

Remove outliers by selecting data points that are within three times the dispersion from the sample median:

Test the new data against standard normal distribution:

Generate data from a Student distribution:

Compute the dispersion of the data with three measures: standard deviation, square root of trimmed variance and dispersion:

Assess the accuracy of these three dispersion estimators via bootstrapping:

estimator gives the smallest spread with the given data:

Properties & Relations (2)

QnDispersion is a rank-based dispersion estimator with its statistic based on pairwise absolute differences:

Pick the positive values among the differences and compute the order statistic using RankedMin:

Compare with QnDispersion with scaling factor equal to 1:

Histogram of pairwise differences with a red line indicating the value of the statistic:

QnDispersion, SnDispersion and StandardDeviation are estimators of the scale parameter of NormalDistribution:

Assess the accuracy of the estimators via bootstrapping:

Compute the relative efficiencies with respect to StandardDeviation, using the estimated results:

Top