InterquartileRange
InterquartileRange[data]
gives the difference between the upper and lower quartiles 
for the elements in data.
InterquartileRange[data,{{a,b},{c,d}}]
uses the quantile definition specified by parameters a, b, c, d.
InterquartileRange[dist]
gives the difference between the upper and lower quartiles 
for the distribution dist.
Details
- InterquartileRange is also known as IQR.
- InterquartileRange is a robust measure of dispersion, which means it is not very sensitive to outliers.
- InterquartileRange[data] is given by
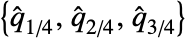, where 
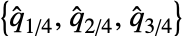is given by Quartiles[data]. » - For MatrixQ data, the interquartile range is computed for each column vector with InterquartileRange[{{x1,y1,…},{x2,y2,…},…}], equivalent to {InterquartileRange[{x1,x2,…}],InterquartileRange[{y1,y2,…}]}. »
- For ArrayQ data, the interquartile range is equivalent to ArrayReduce[InterquartileRange,data,1]. »
- InterquartileRange[data,{{a,b},{c,d}}] uses the Quartiles definition specified by parameters a, b, c, d. »
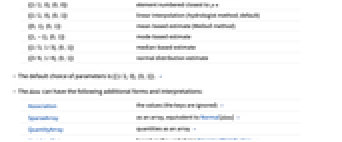
- Common choices of parameters {{a,b},{c,d}} include:
-
{{0, 0}, {1, 0}} inverse empirical CDF {{0, 0}, {0, 1}} linear interpolation (California method) {{1/2, 0}, {0, 0}} element numbered closest to p n {{1/2, 0}, {0, 1}} linear interpolation (hydrologist method; default) {{0, 1}, {0, 1}} mean‐based estimate (Weibull method) {{1, -1}, {0, 1}} mode‐based estimate {{1/3, 1/3}, {0, 1}} median‐based estimate {{3/8, 1/4}, {0, 1}} normal distribution estimate - The default choice of parameters is {{1/2,0},{0,1}}. »
- The data can have the following additional forms and interpretations:
-
Association the values (the keys are ignored) » SparseArray as an array, equivalent to Normal[data] » QuantityArray quantities as an array » WeightedData based on the underlying EmpiricalDistribution » EventData based on the underlying SurvivalDistribution » TimeSeries, TemporalData, … vector or array of values (the time stamps ignored) » Image,Image3D RGB channel's values or grayscale intensity value » Audio amplitude values of all channels » DateObject, TimeObject list of dates or list of times » - InterquartileRange[dist] is given by
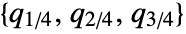, where 
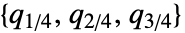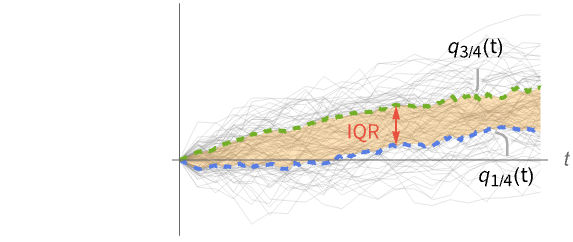
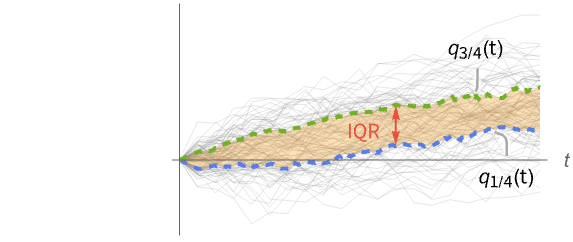
is given by Quartiles[dist]. » - For a random process proc, the interquartile range function can be computed for a slice distribution at time t, SliceDistribution[proc,t], as InterquartileRange[SliceDistribution[proc,t]]. »
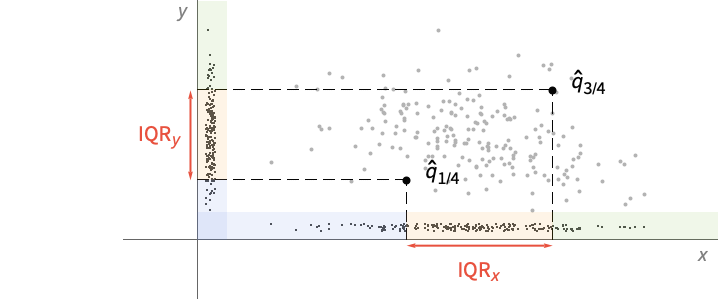
Examples
open allclose allBasic Examples (3)
Scope (22)
Basic Uses (8)
Exact input yields exact output:
Approximate input yields approximate output:
Compute results using other parametrizations:
Find the interquartile range for WeightedData:
Find the interquartile range for EventData:
Find the interquartile range for TemporalData:
Find the interquartile range of TimeSeries:
Array Data (5)
InterquartileRange for a matrix gives columnwise ranges:
Interquartile range for a tensor works across the first index:
When the input is an Association, InterquartileRange works on its values:
SparseArray data can be used just like dense arrays:
Find interquartile range of a QuantityArray:
Image and Audio Data (2)
Date and Time (4)
Applications (6)
InterquartileRange indicates the spread of values:
InterquartileRange can be used as a check for agreement between data and a distribution:
Find the interquartile range of the data:
Compare with the interquartile range of the distribution:
Identify periods of high volatility in stock data using an annual moving interquartile range:
Find the interquartile ranges for the girth, height, and volume of timber, respectively, in 31 felled black cherry trees:
Compute InterquartileRange for slices of a collection of paths of a random process:
Plot of the interquartile range for the selected times:
Find the interquartile range of the heights for the children in a class:
Properties & Relations (4)
InterquartileRange is the difference of linearly interpolated Quantile values:
InterquartileRange is the difference between the first and third quartiles:
QuartileDeviation is half the interquartile range:
BoxWhiskerChart shows the interquartile range for data:
Possible Issues (1)
InterquartileRange requires numeric values in data:
Neat Examples (1)
The distribution of InterquartileRange estimates for 20, 100, and 300 samples:
Text
Wolfram Research (2007), InterquartileRange, Wolfram Language function, https://reference.wolfram.com/language/ref/InterquartileRange.html (updated 2024).
CMS
Wolfram Language. 2007. "InterquartileRange." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/InterquartileRange.html.
APA
Wolfram Language. (2007). InterquartileRange. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InterquartileRange.html