RegionDimension

RegionDimension[reg]

gives the geometric dimension of the region reg.

Details and Options

  • The geometric dimension d of reg is the largest d such that a d-dimensional ball can be completely embedded in the region.
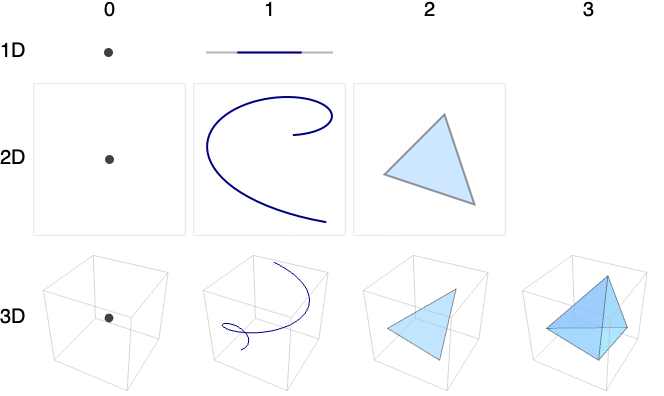
  • Typical names for regions of different dimensions include:
  • 0points
    1lines, curves, arcs, segments, intervals
    2planes, surfaces
    3solids, volumes
  • Example cases with rows corresponding to embedding dimension and columns to RegionDimension:
  • RegionDimension takes an Assumptions option that can be used to specify assumptions on parameters.

Examples

open allclose all

Basic Examples  (4)

The dimension of regions in :

The dimension of regions in :

The dimension of regions in :

The dimension of regions in :

Scope  (17)

Special Regions  (4)

Regions in including Point:

Interval:

Regions in including Point:

Line:

Circle:

Disk:

Regions in including Point:

Line:

Polygon:

Cylinder:

Regions in including Simplex in :

Cuboid in :

Ball in :

Formula Regions  (3)

The dimension of a disk represented as an ImplicitRegion:

A cylinder:

The dimension of a disk represented as a ParametricRegion:

Using a rational parametrization of the disk:

A cylinder:

ImplicitRegion can have several components of different dimension:

RegionDimension gives the largest dimension:

Mesh Regions  (4)

The dimension of a BoundaryMeshRegion:

In 2D:

In 3D:

The dimension of a MeshRegion:

A 3D mesh in 3D:

A 1D mesh embedded in 2D:

A MeshRegion can have components of different dimension:

The RegionDimension is the largest dimension:

Derived Regions  (4)

The dimension of a RegionIntersection:

The dimension of a TransformedRegion:

The dimension of a RegionBoundary:

RegionBoundary for a full-dimensional region is less than the original dimension:

RegionDimension for an intersection can be less than the original dimensions:

The dimension can drop by more than one:

Geographic Regions  (2)

Polygons with GeoPosition:

Polygons with GeoPositionXYZ:

Polygons with GeoPositionENU:

Polygons with GeoGridPosition:

Applications  (8)

A zero-dimensional object is a collection of points:

A one-dimensional object is a collection of curves:

A two-dimensional object is a collection of surfaces:

Use RegionDimension to tell the difference between a volume and a surface:

Regions may be visually identical:

But differ in dimensionality:

Compute dimension of regions that cannot be visualized:

The unit for RegionMeasure is with the length unit and :

Compute the measure of each region:

Compare with the result from RegionMeasure:

Extract MeshRegion primitives by dimension using MeshPrimitives:

Select only full-dimensional primitives:

Properties & Relations  (8)

RegionDimension gives the largest dimension among parts of varying dimension:

The RegionDimension is the largest dimension:

RegionEmbeddingDimension is the dimension of the space in which a region exists:

It is always greater than or equal to RegionDimension:

DimensionalMeshComponents separates a mesh in different dimensional parts:

RegionMeasure and RegionCentroid are dimension dependent:

Integration over a region is dimension dependent:

Since the dimension is 2, integration corresponds to a surface integral:

The RegionDimension of a RegionBoundary is one less than that of the input:

The RegionDimension of a RegionUnion is equal to the largest input dimension:

RegionDimension of a RegionIntersection is no larger than the smallest input dimension:

But it can be smaller:

Wolfram Research (2014), RegionDimension, Wolfram Language function, https://reference.wolfram.com/language/ref/RegionDimension.html.

Text

Wolfram Research (2014), RegionDimension, Wolfram Language function, https://reference.wolfram.com/language/ref/RegionDimension.html.

CMS

Wolfram Language. 2014. "RegionDimension." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RegionDimension.html.

APA

Wolfram Language. (2014). RegionDimension. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RegionDimension.html

BibTeX

@misc{reference.wolfram_2022_regiondimension, author="Wolfram Research", title="{RegionDimension}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/RegionDimension.html}", note=[Accessed: 10-June-2023 ]}

BibLaTeX

@online{reference.wolfram_2022_regiondimension, organization={Wolfram Research}, title={RegionDimension}, year={2014}, url={https://reference.wolfram.com/language/ref/RegionDimension.html}, note=[Accessed: 10-June-2023 ]}