RegionMoment

RegionMoment[reg,{i1,i2,…,in}]

计算区域 reg 的多项式矩 .

更多信息和选项

范例

打开所有单元关闭所有单元

基本范例  (2)

求球体上的多项式矩 ：

求使用区域中参数的相同矩：

求具有不同功效的矩：

范围  (10)

特色区域  (1)

求各种维度的各种特殊区域的矩：

公式区域  (2)

表示为 ImplicitRegion 的圆盘的矩：

圆柱体的矩：

圆盘的矩表示为 ParametricRegion:

使用圆盘的有理参数化表示：

对于圆柱体：

网格区域  (2)

二维空间中，MeshRegion 的矩：

三维空间中：

BoundaryMeshRegion 的矩：

三维空间中：

导出区域  (3)

RegionIntersection 的矩：

TransformedRegion 的矩：

RegionBoundary 的矩：

地理区域  (2)

Polygon 与 GeoPosition 一起使用所得区域的多项式矩：

Polygon 与 GeoGridPosition 一起使用所得区域的多项式矩：

应用  (3)

使用零阶 RegionMoment 求牛的曲面面积：

使用每个轴的一阶矩求质心：

使用 RegionMeasure 和 RegionCentroid 验证结果：

求区域定义的常量密度分布的协方差矩阵：

变换区域，以使得 RegionCentroid 位于原点：

计算二阶矩的矩阵，并且通过除以 RegionMeasure 规范化：

求与牛曲面分享前四阶矩的球体：

球体与牛具有相同的曲面面积和质心：

属性和关系  (8)

曲线的零阶矩等于 ArcLength:

曲面的零阶矩等于 Area:

立体的零阶矩等于 Volume:

任何区域的零阶矩等价于 RegionMeasure:

RegionCentroid 是一阶矩除以零矩：

质心由 给出：

与中心比较：

MomentOfInertia 可以计算惯性矩阵的矩，其中原点为 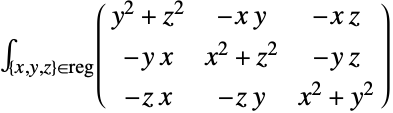，并且包括多个区域矩：

对于 PDF ，Moment 计算 ：

根据均匀密度，RegionMoment 计算 ：

CentralMoment 对于 PDF 和中心 计算 ：

在对齐区域中心后，变成了标准矩：

在前面的例子中，RegionMoment 假定使用均匀分布：

Wolfram Research (2016)，RegionMoment，Wolfram 语言函数，https://reference.wolfram.com/language/ref/RegionMoment.html.

文本

Wolfram Research (2016)，RegionMoment，Wolfram 语言函数，https://reference.wolfram.com/language/ref/RegionMoment.html.

CMS

Wolfram 语言. 2016. "RegionMoment." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/RegionMoment.html.

APA

Wolfram 语言. (2016). RegionMoment. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/RegionMoment.html 年

BibTeX

@misc{reference.wolfram_2024_regionmoment, author="Wolfram Research", title="{RegionMoment}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/RegionMoment.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_regionmoment, organization={Wolfram Research}, title={RegionMoment}, year={2016}, url={https://reference.wolfram.com/language/ref/RegionMoment.html}, note=[Accessed: 22-November-2024 ]}