ResidueSum

ResidueSum[f,z]

有理型関数 f の留数の和を変数 z で求める．

ResidueSum[{f,cons},z]

f の留数の和を制約条件 cons についての解集合内で求める．

詳細とオプション

  • ResidueSumは f のすべての極における留数の和を計算する．極 z0における f の留数は f のローラン(Laurent)展開における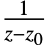の係数として定義される．
  • 留数の和はしばしばコーシー(Cauchy)の留数定理を使った周回積分の計算に使われる．
  • 関数 f は制約条件 cons を満足する x について有理型でなければならない．
  • cons は，等式，不等式あるいはそれらの論理結合を含むことができる．
  • 次は，使用可能なオプションである．
  • Assumptions $Assumptionsパラメータについての仮定
    GenerateConditions Automaticパラメータについての条件を生成するかどうか
    PerformanceGoal $PerformanceGoal速度と品質のどちらを優先するか

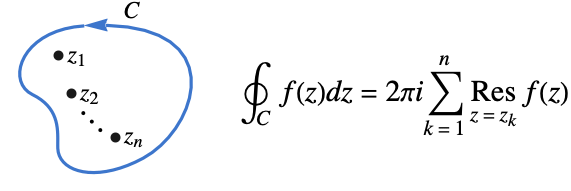
例題

すべて開くすべて閉じる

例  (2)

有理関数の留数の和を求める：

円板上のの留数の和を求める：

スコープ  (6)

有理関数の留数の和：

領域内の有理型関数の留数の和：

無限に多くの極における留数の和は有限である可能性がある：

解析関数には極がない：

はに除去可能な特異点を持つ：

ResidueSumの入力関数は有理型でなければならない：

この関数はのとき有理型である：

オプション  (4)

Assumptions  (1)

パラメータについての条件を指定する：

GenerateConditions  (2)

デフォルトで，ResidueSumは記号パラメータについての条件を生成することがある：

ResidueSumは，GenerateConditionsNoneのときは条件付きの結果は返さず，失敗する：

以下は条件的に有効な結果を条件は述べずに返す：

デフォルトで，一般的に真である条件は報告されない：

GenerateConditions->Trueのときは，すべての条件が報告される：

PerformanceGoal  (1)

PerformanceGoalを使って潜在的に高価な計算を避ける：

デフォルト設定では使用可能なあらゆる手法を使って結果を出そうとする：

アプリケーション  (1)

を単位円に沿って積分する：

単位円板上で の留数の和を計算する：

留数定理を使って積分を計算する：

数値積分の結果と比較する：

特性と関係  (3)

FunctionPolesを使って関数の極を求める：

Residueを使って極における留数を求める：

ResidueSumはすべての極における留数の和を与える：

FunctionMeromorphicを使って関数が有理型かどうかを調べる：

関数が有理型である領域で留数の和を計算する：

FunctionAnalyticを使って関数が複素解析的かどうかを調べる：

解析関数の留数の和は0である：

Wolfram Research (2022), ResidueSum, Wolfram言語関数， https://reference.wolfram.com/language/ref/ResidueSum.html.

テキスト

Wolfram Research (2022), ResidueSum, Wolfram言語関数， https://reference.wolfram.com/language/ref/ResidueSum.html.

CMS

Wolfram Language. 2022. "ResidueSum." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ResidueSum.html.

APA

Wolfram Language. (2022). ResidueSum. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ResidueSum.html

BibTeX

@misc{reference.wolfram_2024_residuesum, author="Wolfram Research", title="{ResidueSum}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/ResidueSum.html}", note=[Accessed: 24-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_residuesum, organization={Wolfram Research}, title={ResidueSum}, year={2022}, url={https://reference.wolfram.com/language/ref/ResidueSum.html}, note=[Accessed: 24-November-2024 ]}