ResidueSum

ResidueSum[f,z]

求亚纯函数 f 与变量 z 的留数之和.

ResidueSum[{f,cons},z]

在约束条件 cons 的解集中求 f 的留数之和.

更多信息和选项

  • ResidueSum 计算 f 的所有极点处留数的和. f 在极点 z0 处的留数被定义为 f 的 Laurent 展开式中 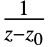的系数.
  • 留数和通常在用柯西留数定理计算围道积分中使用.
  • 函数 f 应为满足约束条件 cons 的 x 的亚纯函数.
  • cons 可以包含等式、不等式或它们的逻辑组合.
  • 可给出以下选项：
  • Assumptions $Assumptions对参数的假设
    GenerateConditions Automatic是否生成针对参数的条件
    PerformanceGoal $PerformanceGoal优先考虑速度还是质量

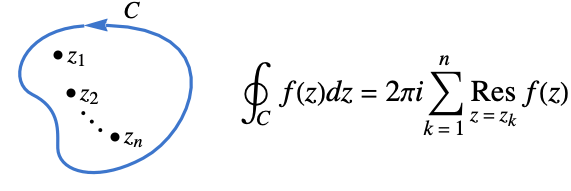
范例

打开所有单元关闭所有单元

基本范例  (2)

求有理函数的留数和：

求 在圆盘内的留数和：

范围  (6)

有理函数的留数和：

亚纯函数在区域内的留数和：

无限多个极点的留数和可能是有限的：

解析函数没有极点：

在 处有可消除的奇点：

ResidueSum 要求输入函数是亚纯函数：

对于 ，函数是亚纯函数：

选项  (4)

Assumptions  (1)

指定参数的条件：

GenerateConditions  (2)

默认情况下，ResidueSum 可能会对符号参数生成条件：

如果设定 GenerateConditionsNone，ResidueSum 将会失败，而不是给出有条件的结果：

下面返回一个在一定条件下有效的结果而不说明条件：

默认情况下，不报告一般为真的条件：

如果设定 GenerateConditions->True，则汇报所有的条件：

PerformanceGoal  (1)

用 PerformanceGoal 避免可能费时的计算：

默认设置使用所有可用的技术来尝试产生结果：

应用  (1)

沿单位圆对 进行积分：

计算 在单位圆盘内的留数和：

用留数定理计算积分：

与数值积分的结果相比较：

属性和关系  (3)

用 FunctionPoles 求函数的极点：

用 Residue 求极点处的留数：

ResidueSum 给出所有极点处留数的和：

用 FunctionMeromorphic 测试函数是否为亚纯函数：

计算函数是亚纯函数的区域中的留数和：

用 FunctionAnalytic 测试函数是否为复解析函数：

解析函数的留数和为零：

Wolfram Research (2022)，ResidueSum，Wolfram 语言函数，https://reference.wolfram.com/language/ref/ResidueSum.html.

文本

Wolfram Research (2022)，ResidueSum，Wolfram 语言函数，https://reference.wolfram.com/language/ref/ResidueSum.html.

CMS

Wolfram 语言. 2022. "ResidueSum." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/ResidueSum.html.

APA

Wolfram 语言. (2022). ResidueSum. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ResidueSum.html 年

BibTeX

@misc{reference.wolfram_2025_residuesum, author="Wolfram Research", title="{ResidueSum}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/ResidueSum.html}", note=[Accessed: 01-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_residuesum, organization={Wolfram Research}, title={ResidueSum}, year={2022}, url={https://reference.wolfram.com/language/ref/ResidueSum.html}, note=[Accessed: 01-April-2025 ]}