ScalingFunctions

ScalingFunctions

ListPlot，BarChart，Histogramおよび他のプロット関数のオプションで，使用するスケーリング関数を指定する．

詳細

  • スケーリング関数はプロットやグラフの要素の外観を変換する．
  • プロット中の枠や軸に示される値はスケーリング関数に基づいて特別に選択される．
  • スケーリング関数はプロットの特徴や動作が見やすくなるように座標を表示するために使われる．
  • 軸やその他のラベルは，通常は，スケールされないもとの値で表示されるため，再スケーリングしなくても直接読める．表示される特定の値はスケーリング関数に依存するので線形間隔ではないかもしれない．
  • ScalingFunctionsでは次の設定値が使える．
  • Noneスケーリング関数は使わない
    "name"名前付きのスケーリング関数を使う
    {f,f-1}スケーリング関数 f とその逆関数の f-1を使う
    {s1,s2,…}方向 i にスケーリング関数指定 siを使う
  • 次は，急速な成長や衰えを示す名前付きの対数スケールである．
  • "Log"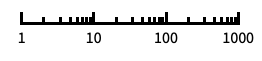自動目盛ラベル付きの対数スケール
    "Log2"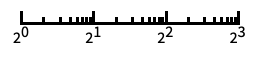目盛が2の累乗で底が2の対数スケール
    "Log10"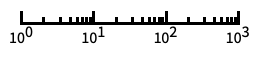目盛が10の累乗で底が10の対数スケール
    "SignedLog"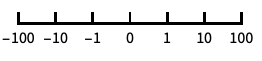0と負の数を含む対数に似たスケール
    {"SignedLog",α}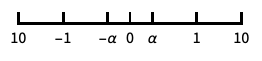0の周りのオフセットが gap の符号付きの対数スケール
  • 次は，特別な名前付きスケールである．
  • "Date"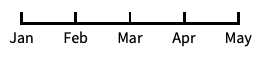日付が目盛のデフォルトの日付スケール
    "Reverse"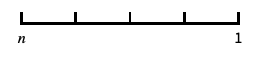座標の方向を逆にする
    "Reciprocal"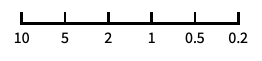逆数スケールを使う
  • 次は，カテゴリ的スケールである．
  • NominalScale[…]項目を識別する
    OrdinalScale[…]順序付けられた項目をランク付ける
  • 次は，無限範囲を有限範囲に圧縮して近似動作を示す名前付きの無限スケールである．
  • "Infinite"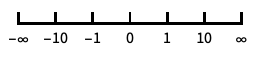デフォルトの無限スケール
    {"Infinite",interval} 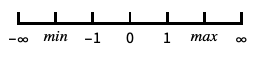interval に焦点を当てた無限スケール
  • 無限領域でプロットする際は，自動的に無限スケールが使われる．
  • オプションは，もとの座標で指定され，スケーリング関数によって自動的に処理される．
  • Ticks，GridLines等はスケールされた位置のスケールされていない値を示す．
  • ScalingFunctions->"Log"のとき，CandlestickChart，RenkoChartおよびその他の金融可視化関数は株価を対数スケールでプロットする．

例題

例  (6)

対数スケール値で関数を示す：

反転された 軸を使う：

対数スケールを高さに使ってBarChartを表示する：

両対数スケールでHistogramを生成する：

データを逆軸でプロットする：

軸が反転していて 軸がワイブル確率スケールのBubbleChartを生成する：

Wolfram Research (2010), ScalingFunctions, Wolfram言語関数， https://reference.wolfram.com/language/ref/ScalingFunctions.html （2021年に更新）.

テキスト

Wolfram Research (2010), ScalingFunctions, Wolfram言語関数， https://reference.wolfram.com/language/ref/ScalingFunctions.html （2021年に更新）.

CMS

Wolfram Language. 2010. "ScalingFunctions." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/ScalingFunctions.html.

APA

Wolfram Language. (2010). ScalingFunctions. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ScalingFunctions.html

BibTeX

@misc{reference.wolfram_2024_scalingfunctions, author="Wolfram Research", title="{ScalingFunctions}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/ScalingFunctions.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_scalingfunctions, organization={Wolfram Research}, title={ScalingFunctions}, year={2021}, url={https://reference.wolfram.com/language/ref/ScalingFunctions.html}, note=[Accessed: 18-November-2024 ]}