ScalingFunctions
更多信息



- 缩放函数改变绘图和图表中元素的外观.
- 图中的框架和轴上显示的值专门根据缩放函数选择.
- 缩放函数用于以更容易查看绘图中的特征或行为的方式显示坐标.
- 轴和其他标签通常使用原始未缩放的值显示,因此可以直接进行读取,而无需进一步重新缩放. 显示的具体值取决于缩放函数并可能不是线性间隔排列.
- ScalingFunctions 的可能设置包括:
-
None 不使用刻度函数 "name" 使用命名的缩放函数 {f,f-1} 使用刻度函数 f 和它的逆函数 f-1 {s1,s2,…} 对于方向 i 使用刻度函数规范 si - 显示快速增长或衰减的命名对数缩放尺度包括:
-
"Log" 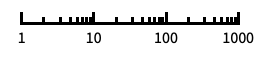
带有自动刻度标记的对数刻度缩放尺度 "Log2" 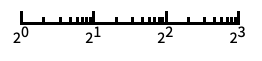
以 2 为底的对数缩放尺度,其刻度为 2 的幂 "Log10" 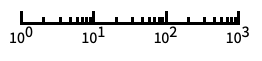
以 10 为底的对数缩放尺度,其刻度为 10 的幂 "SignedLog" 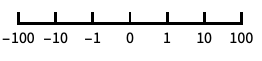
包含 0 和负数的类似对数缩放尺度 {"SignedLog",α} 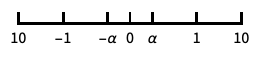
偏移量 α 约为 0 的有符号对数缩放尺度 - 特殊命名的缩放尺度包括:
-
"Date" 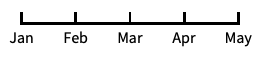
带有日期刻度的默认日期缩放尺度 "Reverse" 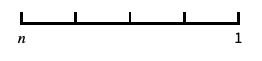
反转坐标方向 "Reciprocal" 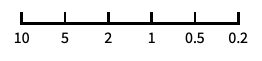
使用倒数缩放 - 分类尺度包括:
-
NominalScale[…] 
识别项目 OrdinalScale[…] 
排序项目 - 通过将无限范围压缩为有限范围来显示渐近行为的命名无限缩放尺度包括:
-
"Infinite" 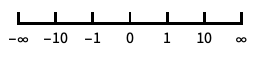
默认无限缩放尺度 {"Infinite",interval} 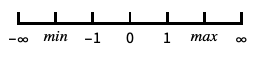
重点关注 interval 的无限缩放尺度 - 在无限域上绘图时会自动使用无限缩放比例.
- 选项使用原始坐标指定,并由缩放函数自动处理.
- Ticks、GridLines 等表示未尺度缩放的值,但是它们位于尺度缩放后的位置上.
- 设置 ScalingFunctions->"Log",CandlestickChart、RenkoChart 以及其它金融可视化函数在对数尺度上绘制价格.
范例
基本范例 (6)
Wolfram Research (2010),ScalingFunctions,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ScalingFunctions.html (更新于 2021 年).
文本
Wolfram Research (2010),ScalingFunctions,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ScalingFunctions.html (更新于 2021 年).
CMS
Wolfram 语言. 2010. "ScalingFunctions." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2021. https://reference.wolfram.com/language/ref/ScalingFunctions.html.
APA
Wolfram 语言. (2010). ScalingFunctions. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ScalingFunctions.html 年