Series[f,{x,x0,n}]
generates a power series expansion for f about the point x=x0 to order (x-x0)n, where n is an explicit integer.
Series[f,xx0]
generates the leading term of a power series expansion for f about the point x=x0.
Series[f,{x,x0,nx},{y,y0,ny},…]
successively finds series expansions with respect to x, then y, etc.


Series
Series[f,{x,x0,n}]
generates a power series expansion for f about the point x=x0 to order (x-x0)n, where n is an explicit integer.
Series[f,xx0]
generates the leading term of a power series expansion for f about the point x=x0.
Series[f,{x,x0,nx},{y,y0,ny},…]
successively finds series expansions with respect to x, then y, etc.
Details and Options

- Series can construct standard Taylor series, as well as certain expansions involving negative powers, fractional powers, and logarithms.
- Series detects certain essential singularities. On[Series::esss] makes Series generate a message in this case.
- Series can expand about the point x=∞.
- Series[f,{x,0,n}] constructs Taylor series for any function f according to the formula
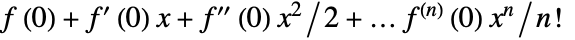 .
. - Series effectively evaluates partial derivatives using D. It assumes that different variables are independent.
- The result of Series is usually a SeriesData object, which you can manipulate with other functions.
- Normal[series] truncates a power series and converts it to a normal expression.
- SeriesCoefficient[series,n] finds the coefficient of the n
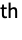 -order term.
-order term. - The following options can be given:
-
Analytic True whether to treat unrecognized functions as analytic Assumptions $Assumptions assumptions to make about parameters SeriesTermGoal Automatic number of terms in the approximation
Examples
open all close allBasic Examples (4)
Scope (10)
Univariate Series (10)
Series can handle fractional powers and logarithms:
Symbolic parameters can often be used:
Laurent series with negative powers can be generated:
Truncate the series to the specified negative power:
Find power series for special functions:
Find the series for a function at a branch point:
With x assumed to be to the left of the branch point, a simpler result is given:
Series can give asymptotic series:
Generalizations & Extensions (4)
Power series in two variables:
Series is threaded element-wise over lists:
Series generates SeriesData expressions:
Series can work with approximate numbers:
Options (4)
Analytic (1)
Series by default assumes symbolic functions to be analytic:
Assumptions (3)
Use Assumptions to specify regions in the complex plane where expansions should apply:
Applications (8)
Plot successive series approximations to ![]() :
:
Find a series expansion for a standard combinatorial problem:
Find Fibonacci numbers from a generating function:
Find Legendre polynomials by expanding a generating function:
Set up a generating function to enumerate ways to make change using U.S. coins:
The number of ways to make change for $1:
Find the lowest-order terms in a large polynomial:
Find higher-order terms in Newton's approximation for a root of f[x] near ![]() :
:
Plot the complex zeros for a series approximation to Exp[x]:
Properties & Relations (10)
Series always only keeps terms up to the specified order:
Operations on series keep only the appropriate terms:
Normal converts to an ordinary polynomial:
Any mathematical function can be applied to a series:
Adding a series of lower order causes the higher-order terms to be dropped:
Solve equations for series coefficients:
Find the list of coefficients in a series:
Use O[x] to force the construction of a series:
ComposeSeries treats a series as a function to apply to another series:
InverseSeries does series reversion to find the series for the inverse function of a series:
Use FunctionAnalytic to test whether a function is analytic:
An analytic function can be expressed as a Taylor series at each point of its domain:
Possible Issues (7)
When there is an essential singularity, Series will attempt to factor it out:
Numeric values cannot be substituted directly for the expansion variable in a series:
Use Normal to get a normal expression in which the substitution can be done:
Series must be converted to normal expressions before being plotted:
Power series with different expansion points cannot be combined:
Not all series are represented by expressions with head SeriesData:
Some functions cannot be decomposed into series of power-like functions:
Series does not change expressions independent of the expansion variable:
Related Guides
Related Links
History
Introduced in 1988 (1.0) | Updated in 2020 (12.1)
Text
Wolfram Research (1988), Series, Wolfram Language function, https://reference.wolfram.com/language/ref/Series.html (updated 2020).
CMS
Wolfram Language. 1988. "Series." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/Series.html.
APA
Wolfram Language. (1988). Series. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Series.html
BibTeX
@misc{reference.wolfram_2025_series, author="Wolfram Research", title="{Series}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/Series.html}", note=[Accessed: 04-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_series, organization={Wolfram Research}, title={Series}, year={2020}, url={https://reference.wolfram.com/language/ref/Series.html}, note=[Accessed: 04-January-2026]}