SolidAngle[p,{u1,…,ud}]
gives the solid angle at the point p and spanned by the vectors u1,…,ud.
SolidAngle[p,reg]
gives the solid angle subtended by the region reg.


SolidAngle
SolidAngle[p,{u1,…,ud}]
gives the solid angle at the point p and spanned by the vectors u1,…,ud.
SolidAngle[p,reg]
gives the solid angle subtended by the region reg.
Details

- SolidAngle is also known as planar angle or spherical angle.
- SolidAngle is typically used to measure the amount of the field of view from a point that an object covers.
- SolidAngle[p,{u1,…,ud}] is the measure of the intersection of the d-dimensional unit sphere Sphere[p] and the conic hull generated by the vectors u1,…,ud.
- SolidAngle[p,reg] is the measure of the intersection of the unit sphere centered at p and half‐lines from p through points of the region reg.
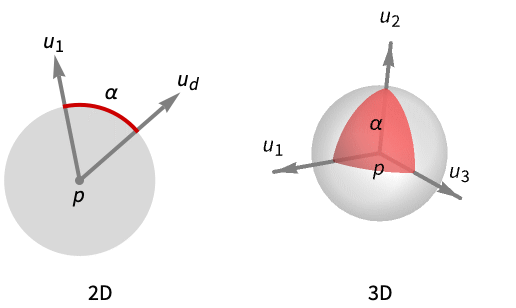
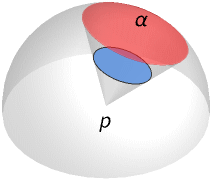
Examples
open all close allBasic Examples (1)
Scope (2)
Use SolidAngle to find the angle at the point and spanned by the vectors:
The solid angle subtended by the Cone[{{1,1,1},{0,0,0}}]:
Properties & Relations (5)
SolidAngle[{0,0},{u1,u2}] is the planar angle between the half‐lines from the point p in the direction of u1 and u2:
SolidAngle[{0,0,0},{u1,u2,u3}] is the surface area of the triangle on the unit sphere with corner points ![]() :
:
In 2D, SolidAngle[p,Line[{q1,q2}]] is equivalent to PlanarAngle[{q1,p,q2}]:
In 3D, SolidAngle[p,reg] is the surface area of the intersection of the unit sphere centered at p that lies in the infinite cone with vertex p and enclosing reg:
SolidAngle[p,{u1,…,ud}] is equivalent to PolyhedronAngle[ℛ,p], where u1,…,ud are vectors adjacent to the point p in a polyhedron ℛ:
See Also
Related Guides
History
Text
Wolfram Research (2019), SolidAngle, Wolfram Language function, https://reference.wolfram.com/language/ref/SolidAngle.html.
CMS
Wolfram Language. 2019. "SolidAngle." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SolidAngle.html.
APA
Wolfram Language. (2019). SolidAngle. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SolidAngle.html
BibTeX
@misc{reference.wolfram_2025_solidangle, author="Wolfram Research", title="{SolidAngle}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/SolidAngle.html}", note=[Accessed: 09-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_solidangle, organization={Wolfram Research}, title={SolidAngle}, year={2019}, url={https://reference.wolfram.com/language/ref/SolidAngle.html}, note=[Accessed: 09-March-2026]}