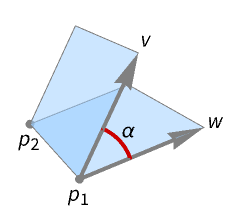
DihedralAngle[{p1,p2},{v,w}]
gives the angle between two half-planes bounded by the line through p1 and p2 and extended in the direction v and w.


DihedralAngle
DihedralAngle[{p1,p2},{v,w}]
gives the angle between two half-planes bounded by the line through p1 and p2 and extended in the direction v and w.
Details
- DihedralAngle is also known as face angle or torsion angle.
- DihedralAngle[{p1,p2},{v,w}] is the length of the arc of the unit circle Circle[p1] on the plane with normal p2-p1 and delimited by the half‐planes HalfPlane[{p1,p2},v] and HalfPlane[{p1,p2},w].
Examples
open all close allScope (2)
Use DihedralAngle to find the angle between two half‐planes:
DihedralAngle works with numeric arguments:
Properties & Relations (2)
Dihedral angle is the planar angle in the plane defined by the normal p2-p1 and a point p1.
DihedralAngle[{p1,p2},{v,w}] is equivalent to PolyhedronAngle[ℛ,{p1,p2}], where v and w are vectors in adjacent faces of {p1,p2} in a polyhedron ℛ:
Possible Issues (1)
DihedralAngle gives generic values for symbolic parameters:
Related Guides
History
Text
Wolfram Research (2019), DihedralAngle, Wolfram Language function, https://reference.wolfram.com/language/ref/DihedralAngle.html.
CMS
Wolfram Language. 2019. "DihedralAngle." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DihedralAngle.html.
APA
Wolfram Language. (2019). DihedralAngle. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DihedralAngle.html
BibTeX
@misc{reference.wolfram_2025_dihedralangle, author="Wolfram Research", title="{DihedralAngle}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/DihedralAngle.html}", note=[Accessed: 07-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_dihedralangle, organization={Wolfram Research}, title={DihedralAngle}, year={2019}, url={https://reference.wolfram.com/language/ref/DihedralAngle.html}, note=[Accessed: 07-January-2026]}