SolidMechanicsPDEComponent
SolidMechanicsPDEComponent[vars,pars]
产生具有变量 vars 和参数 pars 的固体力学 PDE 项.
更多信息


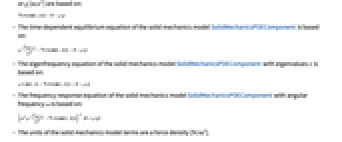
- SolidMechanicsPDEComponent 返回一个用于固体力学分析的微分算子.
- SolidMechanicsPDEComponent 返回要用作偏微分方程一部分的微分算子的总和:
- SolidMechanicsPDEComponent 对受施加载荷和约束的物体产生的位移进行建模.
- SolidMechanicsPDEComponent 为稳态、瞬态、参数、频率响应和特征模态分析创建 PDE 分量.
- SolidMechanicsPDEComponent 模拟固体力学现象,位移
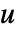 、
、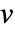 和
和 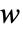 (单位为米 [
(单位为米 [![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/SolidMechanicsPDEComponent.zh/7.png) ])为因变量,
])为因变量,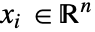 为自变量,单位为 [
为自变量,单位为 [![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/SolidMechanicsPDEComponent.zh/9.png) ],时间变量
],时间变量 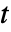 ,单位为秒 [
,单位为秒 [![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/SolidMechanicsPDEComponent.zh/11.png) ],角频率
],角频率 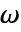 ,单位为弧度/秒.
,单位为弧度/秒. - SolidMechanicsPDEComponent 在两个和三个空间维度中创建 PDE 分量.
- 稳态变量 vars 为 vars={{u[x1,…,xn],v[x1,…,xn],…},{x1,…,xn}}.
- 瞬态或特征模态变量 vars 为 vars={{u[t,x1,…,xn],v[t,x1,…,xn],…},t,{x1,…,xn}}.
- 频率相关变量 vars 是 vars={{u[x1,…,xn],v[x1,…,xn],…},ω,{x1,…,xn}}.
- SolidMechanicsPDEComponent 生成的不同分析类型的方程取决于 vars 的形式.
- 质量密度为
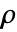 [
[![TemplateBox[{InterpretationBox[, 1], {"kg", , "/", , {"m", ^, 3}}, kilograms per meter cubed, {{(, "Kilograms", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"kg", , "/", , {"m", ^, 3}}, kilograms per meter cubed, {{(, "Kilograms", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/SolidMechanicsPDEComponent.zh/14.png) ],应力张量
],应力张量 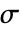 [
[![TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF]](Files/SolidMechanicsPDEComponent.zh/16.png) ],应变张量
],应变张量 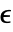 ,位移向量
,位移向量 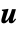 [
[![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/SolidMechanicsPDEComponent.zh/19.png) ],物体的负载向量为
],物体的负载向量为 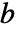 [
[![TemplateBox[{InterpretationBox[, 1], {"N", , "/", , {"m", ^, 3}}, newtons per meter cubed, {{(, "Newtons", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"N", , "/", , {"m", ^, 3}}, newtons per meter cubed, {{(, "Newtons", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/SolidMechanicsPDEComponent.zh/21.png) ] 或
] 或 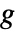 [
[![TemplateBox[{InterpretationBox[, 1], {"m", , "/", , {"s", ^, 2}}, meters per second squared, {{(, "Meters", )}, /, {(, {"Seconds", ^, 2}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"m", , "/", , {"s", ^, 2}}, meters per second squared, {{(, "Meters", )}, /, {(, {"Seconds", ^, 2}, )}}}, QuantityTF]](Files/SolidMechanicsPDEComponent.zh/23.png) ],固体力学偏微分方程 SolidMechanicsPDEComponent 的稳态平衡方程基于
],固体力学偏微分方程 SolidMechanicsPDEComponent 的稳态平衡方程基于 - 固体力学模型 SolidMechanicsPDEComponent 的瞬态平衡方程基于:
- 具有特征值
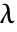 的固体力学模型 SolidMechanicsPDEComponent 的特征频率方程基于:
的固体力学模型 SolidMechanicsPDEComponent 的特征频率方程基于: - 角频率为
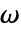 的固体力学模型 SolidMechanicsPDEComponent 的频率响应方程基于:
的固体力学模型 SolidMechanicsPDEComponent 的频率响应方程基于: - 固体力学模型项的单位是力密度
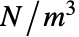 .
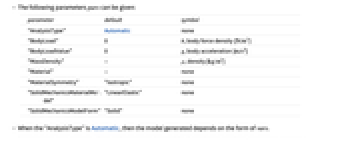
. - 可以给出以下参数 pars:
-
参数 默认值 符号 "AnalysisType" Automatic 无 "BodyLoad" 0 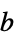 ,体力密度,单位为 [
,体力密度,单位为 [![TemplateBox[{InterpretationBox[, 1], {"N", , "/", , {"m", ^, 3}}, newtons per meter cubed, {{(, "Newtons", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"N", , "/", , {"m", ^, 3}}, newtons per meter cubed, {{(, "Newtons", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/SolidMechanicsPDEComponent.zh/32.png) ]
]
"BodyLoadValue" 0 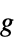 ,体加速度,单位为 [
,体加速度,单位为 [![TemplateBox[{InterpretationBox[, 1], {"m", , "/", , {"s", ^, 2}}, meters per second squared, {{(, "Meters", )}, /, {(, {"Seconds", ^, 2}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"m", , "/", , {"s", ^, 2}}, meters per second squared, {{(, "Meters", )}, /, {(, {"Seconds", ^, 2}, )}}}, QuantityTF]](Files/SolidMechanicsPDEComponent.zh/34.png) ]
]
"MassDensity" - 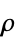 ,密度,单位为 [
,密度,单位为 [![TemplateBox[{InterpretationBox[, 1], {"kg", , "/", , {"m", ^, 3}}, kilograms per meter cubed, {{(, "Kilograms", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"kg", , "/", , {"m", ^, 3}}, kilograms per meter cubed, {{(, "Kilograms", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/SolidMechanicsPDEComponent.zh/36.png) ]
]
"Material" - 无 "MaterialSymmetry" "Isotropic" 无 "SolidMechanicsMaterialModel" "LinearElastic" 无 "SolidMechanicsModelForm" "Solid" 无 - 当 "AnalysisType" 为 Automatic 时,则生成的模型取决于 vars 的形式.
- 对于特征频率分析,"AnalysisType" 需要设置为 "Eigenmode",并且需要使用时间相关变量 tvars.
- 如果指定了 "Material",则材料常数从材料数据中提取; 否则,需要指定相关的材料参数.
- 对于线性弹性各向同性材料,可以使用任意两个模量:
-
参数名称 "BulkModulus" "LameParameter" "PoissonRatio" "PWaveModulus" "ShearModulus" "YoungModulus" - 参数 "SolidMechanicsModelForm" 可以是 "Solid"、"PlaneStress" 或 "PlaneStrain".
- 对于 "PlaneStress" 和 "PlaneStress" 模型,需定义 "Thickness" 参数.
- 默认材料模型是线性弹性各向同性材料模型.
- 线性弹性小变形模型可使用以下材料对称性:
-
材料对称性名称 "Isotropic" "Orthotropic" "TransverselyIsotropic" "Anisotropic" - 系统提供以下各向同性可压缩超弹性大变形材料模型:
-
材料模型名称 "StVenantKirchhoff" "NeoHookean" - 系统提供以下近各向同性不可压缩超弹性大变形材料模型:
-
材料模型名称 "ArrudaBoyce" "Gent" "MooneyRivlin" "NeoHookean" "Yeoh" - 动力学方程使用无穷小、小变形应变度量:
- 对于非线性材料定律,运动方程使用基于变形梯度
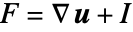 的 Green–Lagrange 应变度量,其中,
的 Green–Lagrange 应变度量,其中,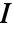 是单位矩阵:
是单位矩阵: - 线弹性材料模型的本构方程由下式给出,其中弹性矩阵为
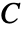 ,初始应力为
,初始应力为 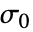 ,初始应变为
,初始应变为 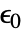 ,热应变为
,热应变为 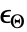 :
: - 法向应变分量
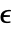 和剪切应变分量
和剪切应变分量 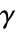 使用 Voigt 标记法,顺序如下:
使用 Voigt 标记法,顺序如下: - 正应力分量
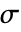 和剪应力分量
和剪应力分量 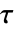 使用 Voigt 标记法,顺序如下:
使用 Voigt 标记法,顺序如下: - "PlaneStrain" 模型对于
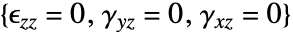 假设
假设 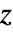 方向的应变为 0.
方向的应变为 0. - "PlaneStress" 模型对于
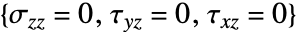 假设
假设 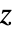 方向的应力为 0.
方向的应力为 0. - "RegionSymmetry""Axisymmetric" 使用截断圆柱坐标系,并假定
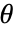 方向的位移
方向的位移 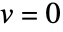 ,
,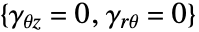 . 注意
. 注意 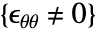 .
. - 具有杨氏模量
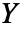 和泊松比
和泊松比 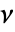 的线弹性各向同性材料的本构方程由下式给出:
的线弹性各向同性材料的本构方程由下式给出: - 可添加热应变
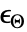 ,其热膨胀系数为
,其热膨胀系数为 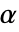 ,单位为 [
,单位为 [![1TemplateBox[{InterpretationBox[, 1], {"/", , "K"}, reciprocal kelvins, {1, /, {(, "Kelvins", )}}}, QuantityTF] 1TemplateBox[{InterpretationBox[, 1], {"/", , "K"}, reciprocal kelvins, {1, /, {(, "Kelvins", )}}}, QuantityTF]](Files/SolidMechanicsPDEComponent.zh/65.png) ],热应变温度为
],热应变温度为  [
[![TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF]](Files/SolidMechanicsPDEComponent.zh/67.png) ],热应变参考温度为
],热应变参考温度为 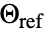 [
[![TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF]](Files/SolidMechanicsPDEComponent.zh/69.png) ]:
]: - 可以为 "LinearElastic" "Isotropic" 材料模型提供以下子参数:
-
参数 默认值 符号 "InitialStrain" 0 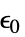 ,初始应变
,初始应变"InitialStress" 0 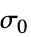 ,初始应力 [
,初始应力 [![TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF]](Files/SolidMechanicsPDEComponent.zh/73.png) ]
]"PoissonRatio" Automatic 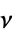 ,泊松比
,泊松比"ThermalExpansion" 0 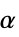 ,热膨胀系数 [
,热膨胀系数 [![1TemplateBox[{InterpretationBox[, 1], {"/", , "K"}, reciprocal kelvins, {1, /, {(, "Kelvins", )}}}, QuantityTF] 1TemplateBox[{InterpretationBox[, 1], {"/", , "K"}, reciprocal kelvins, {1, /, {(, "Kelvins", )}}}, QuantityTF]](Files/SolidMechanicsPDEComponent.zh/76.png) ]
]"ThermalStrainTemperature" 0 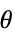 ,温度 [
,温度 [![TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF]](Files/SolidMechanicsPDEComponent.zh/78.png) ]
]"ThermalStrainReferenceTemperature" 0 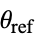 ,温度 [
,温度 [![TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF]](Files/SolidMechanicsPDEComponent.zh/80.png) ]
]"YoungModulus" Automatic 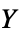 ,杨氏模量 [
,杨氏模量 [![TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF]](Files/SolidMechanicsPDEComponent.zh/82.png) ]
] - 具有柔量矩阵
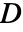 的线弹性正交各向异性材料模型的本构方程为:
的线弹性正交各向异性材料模型的本构方程为: - 弹性矩阵是柔量矩阵的逆矩阵
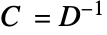 .
. - 具有剪切模量
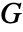 的线性弹性正交各向异性柔量矩阵
的线性弹性正交各向异性柔量矩阵 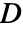 由下式给出:
由下式给出: - 对于线弹性正交各向异性材料模型,热膨胀系数
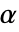 取决于方向:
取决于方向: - 可以为 "LinearElastic" "Orthotropic" 材料模型提供以下子参数:
-
参数 默认值 符号 "InitialStrain" 0 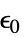 ,初始应变
,初始应变"InitialStress" 0 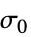 ,初始应力 [
,初始应力 [![TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF]](Files/SolidMechanicsPDEComponent.zh/93.png) ]
]"PoissonRatio" - 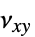 、
、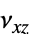 、
、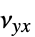 、
、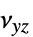 、
、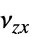 、
、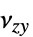 泊松比
泊松比"ShearModulus" - 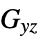 、
、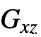 、
、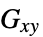 剪切模量 [
剪切模量 [![TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF]](Files/SolidMechanicsPDEComponent.zh/103.png) ]
]"ThermalExpansion" 0 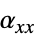 、
、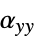 、
、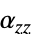 ,热膨胀系数 [
,热膨胀系数 [![TemplateBox[{{InterpretationBox[, 1], 1}, {"/", , "K"}, reciprocal kelvins, {1, /, {(, "Kelvins", )}}}, QuantityTF] TemplateBox[{{InterpretationBox[, 1], 1}, {"/", , "K"}, reciprocal kelvins, {1, /, {(, "Kelvins", )}}}, QuantityTF]](Files/SolidMechanicsPDEComponent.zh/107.png) ]
]"ThermalStrainTemperature" 0 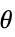 ,温度 [
,温度 [![TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF]](Files/SolidMechanicsPDEComponent.zh/109.png) ]
]"ThermalStrainReferenceTemperature" 0 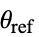 ,温度 [
,温度 [![TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF]](Files/SolidMechanicsPDEComponent.zh/111.png) ]
]"YoungModulus" - 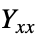 、
、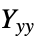 、
、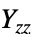 杨氏模量 [
杨氏模量 [![TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF]](Files/SolidMechanicsPDEComponent.zh/115.png) ]
] - 泊松比、剪切模量和杨氏模量被指定为正式的索引变量.
- 对于各向异性材料模型,需要指定全弹性矩阵
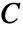 :
: - 或者,可以指定合规矩阵
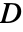 .
. - 对于线弹性各向异性材料模型,热膨胀系数
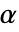 取决于方向:
取决于方向: - 可以为 "LinearElastic" "Anisotropic" 材料模型提供以下子参数:
-
参数 默认值 符号 "ComplianceMatrix" - 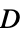 ,柔度矩阵
,柔度矩阵"ElasticityMatrix" - 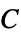 ,弹性矩阵,
,弹性矩阵,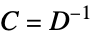
"InitialStrain" 0 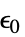 ,初始应变
,初始应变"InitialStress" 0 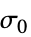 ,初始应力 [
,初始应力 [![TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF]](Files/SolidMechanicsPDEComponent.zh/126.png) ]
]"ThermalExpansion" 0 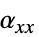 、
、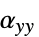 、
、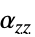 、
、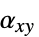 、
、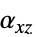 ,
,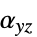 ,热膨胀系数 [
,热膨胀系数 [![TemplateBox[{{InterpretationBox[, 1], 1}, {"/", , "K"}, reciprocal kelvins, {1, /, {(, "Kelvins", )}}}, QuantityTF] TemplateBox[{{InterpretationBox[, 1], 1}, {"/", , "K"}, reciprocal kelvins, {1, /, {(, "Kelvins", )}}}, QuantityTF]](Files/SolidMechanicsPDEComponent.zh/133.png) ]
]"ThermalStrainTemperature" 0 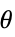 ,温度 [
,温度 [![TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF]](Files/SolidMechanicsPDEComponent.zh/135.png) ]
]"ThermalStrainReferenceTemperature" 0 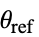 ,温度 [
,温度 [![TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF]](Files/SolidMechanicsPDEComponent.zh/137.png) ]
] - 系统提供可压缩和近不可压缩超弹性材料模型. 可用的情况下,默认值是近不可压缩模型.
- "ArrudaBoyce" 材料模型基于能量密度函数
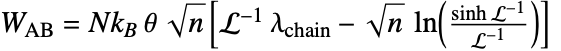 ,其中
,其中 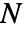 是网络中聚合物链的数量,
是网络中聚合物链的数量,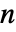 是单个链中链段的数量,
是单个链中链段的数量,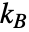 是 Boltzmann 常数,
是 Boltzmann 常数,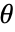 是绝对温度,
是绝对温度,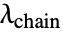 是链的拉伸,
是链的拉伸,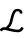 是 Langevin 函数.
是 Langevin 函数. - "Gent" 材料模型基于能量密度函数
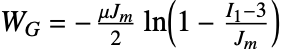 ,其中,
,其中,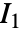 是第一应变不变量,
是第一应变不变量, 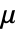 是剪切模量,
是剪切模量,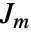 是极限值.
是极限值. - "NeoHookean" 材料模型基于能量密度函数
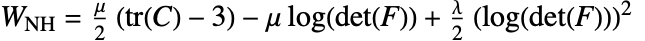 ,其中,
,其中,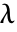 是拉梅第一常数,
是拉梅第一常数,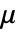 是第二常数,
是第二常数,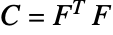 是右 Cauchy–Green 张量,
是右 Cauchy–Green 张量,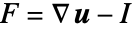 是变形梯度.
是变形梯度. - 可压缩的 "StVenantKirchhoff" 材料模型基于能量密度函数
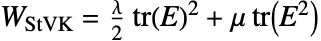 ,其中,
,其中,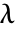 是拉梅第一常数,
是拉梅第一常数,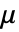 是第二常数,
是第二常数,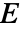 是 Green–Lagrange 应变.
是 Green–Lagrange 应变. - "MooneyRivlin" 材料模型基于能量密度函数
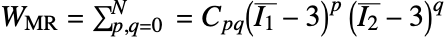 ,其中,
,其中,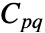 是材料系数,
是材料系数,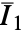 和
和 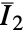 是第一和第二等容应变不变量.
是第一和第二等容应变不变量. - "Yeoh" 材料模型基于能量密度函数
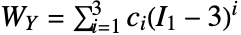 ,其中,
,其中,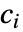 是模型常数,
是模型常数,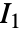 是第一不变量.
是第一不变量. - 可用的情况下,模型的 "Compressibility" 可被指定为 "NearlyIncompressibile" 或 "Compressibile".
- 近不可压缩性以添加到应变能量密度函数
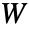 的静水压力
的静水压力 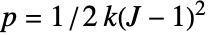 来实现,其中,
来实现,其中,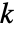 是材料的体积模量.
是材料的体积模量. - 可为所有超弹性模型提供 平面应变和平面应力 模型形式.
- 所有超弹性材料模型可利用标准增强材料模型,来模拟横向各向同性材料,如纤维增强材料.
- SolidMechanicsPDEComponent 使用 "SIBase" 单位. 几何形状必须采用与偏微分方程相同的单位.
- 如果 SolidMechanicsPDEComponent 依赖于在关联 pars(形为 …,keypi…,pivi,…]) 中指定的参数
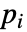 ,则用
,则用 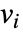 替换参数
替换参数 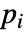 .
.
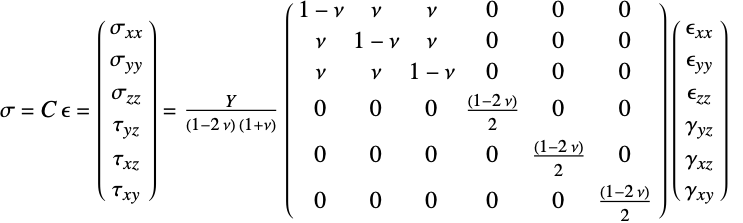
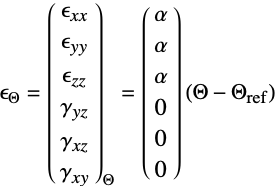
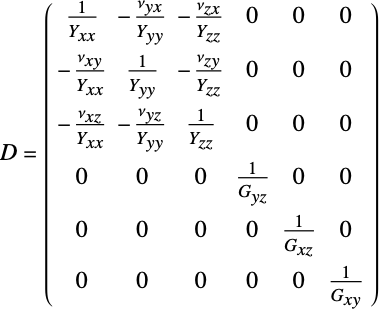
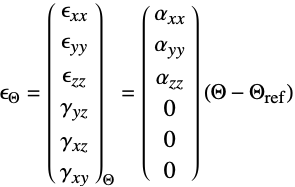
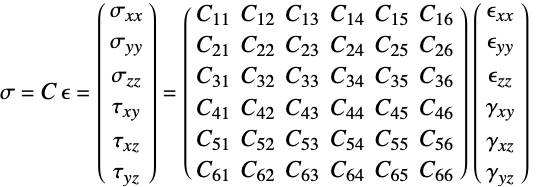
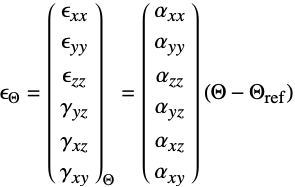
范例
打开所有单元关闭所有单元范围 (19)
稳态平面应力分析 (3)
时变分析 (3)
超弹性材料模型 (2)
纤维增强材料模型 (1)
多材料模型 (1)
Wolfram Research (2021),SolidMechanicsPDEComponent,Wolfram 语言函数,https://reference.wolfram.com/language/ref/SolidMechanicsPDEComponent.html (更新于 2024 年).
文本
Wolfram Research (2021),SolidMechanicsPDEComponent,Wolfram 语言函数,https://reference.wolfram.com/language/ref/SolidMechanicsPDEComponent.html (更新于 2024 年).
CMS
Wolfram 语言. 2021. "SolidMechanicsPDEComponent." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/SolidMechanicsPDEComponent.html.
APA
Wolfram 语言. (2021). SolidMechanicsPDEComponent. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/SolidMechanicsPDEComponent.html 年