Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

SolidMechanicsStress

SolidMechanicsStress[vars,pars,strain]

生成包含变量 vars、参数 pars 和总应变 strain 的固体力学内应力.

SolidMechanicsStress[vars,pars,strain,displacement]

生成非线性材料定律的固体力学应力.

更多信息

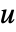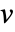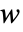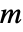SolidMechanicsStress 以为单位的因变量位移、和，以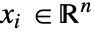为单位的自变量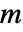，以及以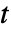为单位的时间变量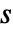，返回给定总应变的力学应力.

应力是单位横截面积上的阻力 .
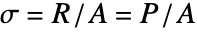应力的单位是 .
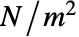SolidMechanicsStress 使用与 SolidMechanicsPDEComponent 一样的变量 vars 指定.
SolidMechanicsStress 使用与 SolidMechanicsPDEComponent 一样的参数 pars 指定.
用 SymmetrizedArray 指定 strain.
通常情况下，strain 是 SolidMechanicsStrain 的结果.
对于弹性材料，SolidMechanicsStress 使用弹性应变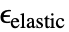来计算应力：

SolidMechanicsStress 从给定的总应变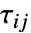中减去热应变或初始应变等非弹性应变 .
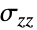SolidMechanicsStress 返回以下形式的应力 SymmetrizedArray：

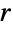表示法向应力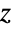，表示剪切应力.
SolidMechanicsStress 计算内应力：

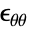可以使用 "InitialStress" 参数为 SolidMechanicsPDEComponent 指定初始应力 .
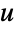对于非线性材料，SolidMechanicsStress 使用总应变和位移来计算应力.

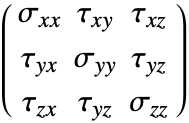
范例

打开所有单元关闭所有单元

基本范例 (1)

计算应变造成的应力：

可视化应力：

范围 (4)

稳态分析 (1)

计算末端固定并在顶部施加力的勺子的挠度. 设置变量和参数：

设置 PDE 和几何形状：

计算位移造成的应变：

计算应变造成的应力：

可视化应力：

稳态平面应力分析 (1)

作为扩展模型计算平面应力的例子. 这样可以计算平面外应变，并验证平面外应力为 0. 矩形钢板左侧固定，右侧有强制位移. 设置区域、变量和参数. 现在变量包括所有三个方向：

用三个半自变量求解方程：

请注意，现在位移列表中有三个输出变量. 查看主要变量的位移：

计算应变：

请注意，应变是一个 3×3 阵列. 可视化平面外应变：

根据应变计算应力：

请注意，应力是一个 3×3 的数组. 验证平面应力条件：

稳态平面应变分析 (1)

作为扩展模型计算平面应变的例子. 这样就可以计算平面外应力，并验证平面外应变为 0. 设置区域、变量和参数. 现在变量包括所有三个方向：

设置固体力学 PDE 分量：

设置 PDE：

求解 PDE：

根据位移计算应变：

请注意，应变是一个 3×3 阵列. 验证平面应变条件：

根据应变计算应力：

请注意，应力是一个 3×3 的数组. 可视化平面外应力：

稳态超弹性平面应力分析 (1)

计算左侧固定并在右侧施加力的矩形橡胶板的位移. 设置区域、变量和参数：

解方程：

可视化位移：

计算位移造成的应变：

根据应变和位移计算应力：

可视化应变：

可能存在的问题 (1)

在轴对称情况下，指定的位移必须是空间坐标的函数. 为了说明原因，创建不是空间函数的变量、参数和位移函数：

请注意，生成的 InterpolatingFunction 并不是空间坐标和的函数. 现在计算应变和应力时，可以看到在应力张量中也出现了一些没有空间坐标的插值函数：

这是因为在轴对称情况的公式中，应变的分量计算为，其中是第一因变量，是圆柱坐标系中的径向. 推导过程见轴对称模型一节. 根据应变计算应力时，值取自第一个给定的位移函数，本例中为 usol. 如果该函数不依赖于自变量和，则它们不会出现在输出中.

为了避免这种情况，需要在位移中使用空间坐标和：

现在，应力张量的所有 InterpolatingFunction 分量都使用了空间坐标：

顶部