TriangleMeasurement

TriangleMeasurement[tri,type]

gives the specified type of measurement for the triangle tri.

Details

  • The triangle tri can be given as {p1,p2,p3}, Triangle[{p1,p2,p3}] or Polygon[{p1,p2,p3}].
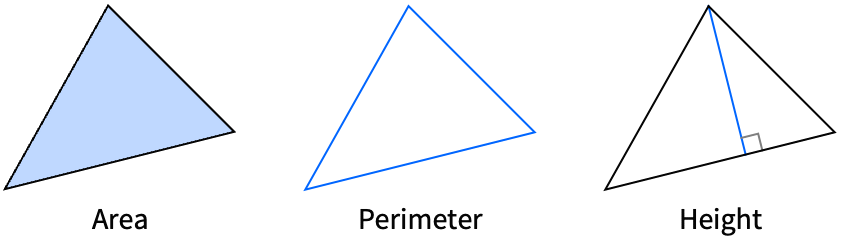
  • The following measurement types can be given:
  • "Area"area
    "Circumradius"radius of circumcircle
    {"Exradius",p}radius of excircle opposite vertex p
    {"ExteriorAngle",p}exterior angle at vertex p
    {"FullExteriorAngle",p}full exterior angle at vertex p
    {"Height",p}height of the triangle measured from vertex p
    "Inradius"radius of incircle
    {"InteriorAngle",p}interior angle at vertex p
    "NinePointRadius"radius of nine-point circle
    "Perimeter"perimeter
    "Semiperimeter"semiperimeter
  • In the form {"type",p}, p can be a symbolic point specification in a GeometricScene, or it can be an explicit vertex of the form {x,y}, Point[{x,y}] or the index i of the vertex. When given in the short form "type", the vertex p2 is used.
  • In any form that specifies a vertex p, a value of All will return a list of three values corresponding to the vertices.
  • TriangleMeasurement can be used with symbolic points in GeometricScene.

Examples

open allclose all

Basic Examples  (2)

Calculate the semiperimeter of a triangle:

Calculate the exradius of a triangle at the specified vertex:

Calculate all of the exradii:

Scope  (11)

Calculate the area of a triangle:

Calculate the area using symbolic coordinates:

Calculate the circumradius of a triangle:

Calculate the exradius of a triangle at the specified vertex:

Calculate the exterior angle of a triangle at the specified vertex:

Calculate the full exterior angle of a triangle at the specified vertex:

Calculate the height of a triangle:

Calculate the inradius of a triangle:

Calculate the interior angle of a triangle at the specified vertex:

Calculate the nine-point center of a triangle:

Calculate the perimeter of a triangle:

Calculate the semiperimeter of a triangle:

Properties & Relations  (11)

TriangleMeasurement[{a,b,c},"Area"] is equivalent to Area[Triangle[{a,b,c}]]:

TriangleConstruct[{a,b,c},"Circumcircle"] is equivalent to Circle[TriangleCenter[{a,b,c},"Circumcenter"],TriangleMeasurement[{a,b,c},"Circumradius"]]:

TriangleConstruct[{a,b,c},"Excircle"] is equivalent to Circle[TriangleCenter[{a,b,c},"Excenter"],TriangleMeasurement[{a,b,c},"Exradius"]]:

TriangleConstruct[{a,b,c},"ExteriorAngle"] is equivalent to PlanarAngle[{a,b,c},"Exterior"]:

TriangleConstruct[{a,b,c},"FullExteriorAngle"] is equivalent to PlanarAngle[{a,b,c},"FullExterior"]:

TriangleMeasurement[{a,b,c},"Height"] is equivalent to ArcLength[TriangleConstruct[{a,b,c},"Altitude"]]:

TriangleConstruct[{a,b,c},"Incircle"] is equivalent to Circle[TriangleCenter[{a,b,c},"Incenter"],TriangleMeasurement[{a,b,c},"Inradius"]]:

TriangleConstruct[{a,b,c},"InteriorAngle"] is equivalent to PlanarAngle[{a,b,c},"Interior"]:

TriangleConstruct[{a,b,c},"NinePointCircle"] is equivalent to Circle[TriangleCenter[{a,b,c},"NinePointCenter"],TriangleMeasurement[{a,b,c},"NinePointRadius"]]:

TriangleConstruct[{a,b,c},"Perimeter"] is equivalent to Perimeter[Triangle[{a,b,c}]]:

TriangleConstruct[{a,b,c},"Semiperimeter"] is equivalent to Perimeter[Triangle[{a,b,c}]]/2:

Wolfram Research (2019), TriangleMeasurement, Wolfram Language function, https://reference.wolfram.com/language/ref/TriangleMeasurement.html.

Text

Wolfram Research (2019), TriangleMeasurement, Wolfram Language function, https://reference.wolfram.com/language/ref/TriangleMeasurement.html.

CMS

Wolfram Language. 2019. "TriangleMeasurement." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/TriangleMeasurement.html.

APA

Wolfram Language. (2019). TriangleMeasurement. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TriangleMeasurement.html

BibTeX

@misc{reference.wolfram_2025_trianglemeasurement, author="Wolfram Research", title="{TriangleMeasurement}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/TriangleMeasurement.html}", note=[Accessed: 18-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_trianglemeasurement, organization={Wolfram Research}, title={TriangleMeasurement}, year={2019}, url={https://reference.wolfram.com/language/ref/TriangleMeasurement.html}, note=[Accessed: 18-April-2025 ]}