PolygonAngle

PolygonAngle[poly]

gives a list of angles at the vertex points of poly.

PolygonAngle[poly,p]

gives the angle at the vertex point p of a polygon poly.

PolygonAngle[poly,i]

gives the angle at the point pi of poly in canonical form Polygon[{p1,…,pn},data].

PolygonAngle[…,"spec"]

gives the angle specified by "spec".

Details

  • PolygonAngle is also known as interior angle.
  • PolygonAngle[poly, p] gives the angle delimited by the two adjacent sides intersecting at p.
  • The following specifications "spec" can be given:
  • "Interior"interior (inside) angle at p
    "Exterior"exterior angle at p
    "FullExterior"full exterior angle at p
  • PolygonAngle[poly,p,"Interior"] is equivalent to PolygonAngle[poly,p].
  • PolygonAngle[poly,p,"Exterior"] is equivalent to π-PolygonAngle[poly,p].
  • PolygonAngle[poly,p,"FullExterior"] is equivalent to 2π-PolygonAngle[poly,p].
  • PolygonAngle can be used with symbolic polygons in GeometricScene.

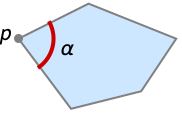
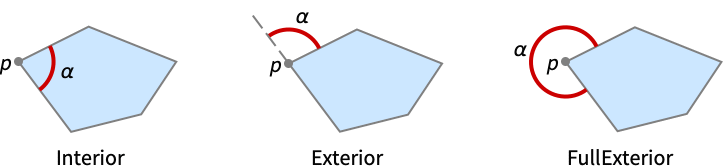
Examples

open allclose all

Basic Examples  (2)

The list of angles at the vertex points:

The angle at the vertex point {-2,0}:

The angle at the point 1 of ℛ in canonical form:

Scope  (6)

Basic Uses  (3)

Use PolygonAngle to find the list of angles at the vertex points:

The angle at the vertex point:

PolygonAngle works on polygons:

Parallelogram:

RegularPolygon:

PolygonAngle works on polygons with GeoGridPosition:

Specifications  (3)

"Interior"  (1)

The interior angle of a polygon at the vertex points:

"Exterior"  (1)

The exterior angle of a polygon at the vertex points:

"FullExterior"  (1)

The full exterior angle of a polygon at the vertex points:

Properties & Relations  (2)

The sum of interior angles of a regular polygon is :

PolygonAngle[ℛ, p] is equivalent to PlanarAngle[p->{q1,q2}] where q1 and q2 are adjacent points of p in a polygon ℛ:

Wolfram Research (2019), PolygonAngle, Wolfram Language function, https://reference.wolfram.com/language/ref/PolygonAngle.html.

Text

Wolfram Research (2019), PolygonAngle, Wolfram Language function, https://reference.wolfram.com/language/ref/PolygonAngle.html.

CMS

Wolfram Language. 2019. "PolygonAngle." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PolygonAngle.html.

APA

Wolfram Language. (2019). PolygonAngle. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PolygonAngle.html

BibTeX

@misc{reference.wolfram_2024_polygonangle, author="Wolfram Research", title="{PolygonAngle}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/PolygonAngle.html}", note=[Accessed: 16-January-2025 ]}

BibLaTeX

@online{reference.wolfram_2024_polygonangle, organization={Wolfram Research}, title={PolygonAngle}, year={2019}, url={https://reference.wolfram.com/language/ref/PolygonAngle.html}, note=[Accessed: 16-January-2025 ]}