UnsameQ

lhs=!=rhs

式 lhs と rhs が等しくない場合にTrueを，その他の場合にFalseを返す．

詳細

  • e1=!=e2=!=e3 は，eiのいずれもが等しくない場合に限りTrueを与える．
  • UnsameQ[]とUnsameQ[expr]は常にTrueを与える． »

予備知識

  • UnsameQ[expr1,expr2]は，expr1が expr2と同一ではないときにはTrueを返し，それ以外の場合はFalseを返す．具体的には，UnsameQ[expr1,expr2]はSameQ[expr1,expr2]がTrueを返すとき（つまり，実数は二進表記の最終桁が違っていてもSameQであるとみなされるという例外を除き，式 expr1と式 expr2のFullForm表現間に厳密な対応関係があるとき）かつそのときに限りFalseを返す．UnsameQ[expr1,expr2]は expr1=!=expr2と入力することができる．複数の引数がある形のUnsameQ[expr1,expr2,…]（expr1=!=expr2=!=…と入力）は，式 expriの中に等しいものがない場合にTrueを返す．
  • 入力形が異なる式も，もとになっている表現が同じであればUnsameQではない．例えば，n! =!=Factorial[n]はFalseを返す．一方，UnsameQは数値的には等しいが表現が異なる数を区別する．例えば，UnsameQ[1,1.]とUnsameQ[1.,1.+0.I]は両方ともTrueを返す．この動作は，等価検定を実行して解決がつかない場合は未評価で返すUnequalの動作とは明白に異なる．
  • UnsameQは他の数多くのシンボルと関係がある．Unequal[expr1,expr2]（expr1!=expr2または expr1≠expr2と入力）は，expr1と expr2が数値的に等しくなければTrueを返す．SameQ（ expr1===expr2と入力）はUnsameQの逆関数である．
  • PossibleZeroQを使って，UnsameQがTrueを返すときに与えられた式の値が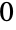になることがあるかどうかを示すことができる．例えば，UnsameQ[Erf[Log[4]+2Log[Sin[Pi/8]]]-Erf[Log[2-Sqrt[2]]],0]はTrueを返すが，この第1引数にPossibleZeroQを呼ぶと（0値は厳密には実証できないという有益なメッセージとともに）Trueを返してこれが0と等しいことが示される．Simplify，FullSimplify，RootReduce等の記号簡約子を使って，UnsameQとUnequal（あるいはSameQとEqual）にとって不可能な（上に挙げた例を含む）等価性を厳密に実証することができることもある．

例題

すべて開くすべて閉じる

例  (2)

2つの式が等価ではないかどうかテストする：

!=はリテラル値が与えられなければ記号のままにする：

完全形：

スコープ  (3)

文字列が等価かどうかテストする：

異なった表現方法の数字は同じではない：

!=はそれでも両者を等価として扱う：

複数の式がすべて互いに異なるかどうかテストする：

アプリケーション  (1)

完全に反対称のテンソルの恒久的な相似形を構築する：

置換された位置に1が現れている：

特性と関係  (4)

UnsameQは任意数の引数を取ることができる：

UnsameQ[expri,exprj]がすべての i と j についてTrueなら，UnsameQ[expr1,expr2,…]はTrueを与える：

一方の式が他方と同じなら，UnsameQはFalseを与える：

UnsameQ[expr1,expre2]は!SameQ[expr1,expr2]に等しい：

UnsameQ[…]と!SameQ[…]は，引数が2つのとき以外は等価ではない：

UnsameQ[]とUnsameQ[expr]は常にTrueを返す：

Wolfram Research (1991), UnsameQ, Wolfram言語関数， https://reference.wolfram.com/language/ref/UnsameQ.html.

テキスト

Wolfram Research (1991), UnsameQ, Wolfram言語関数， https://reference.wolfram.com/language/ref/UnsameQ.html.

CMS

Wolfram Language. 1991. "UnsameQ." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/UnsameQ.html.

APA

Wolfram Language. (1991). UnsameQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/UnsameQ.html

BibTeX

@misc{reference.wolfram_2024_unsameq, author="Wolfram Research", title="{UnsameQ}", year="1991", howpublished="\url{https://reference.wolfram.com/language/ref/UnsameQ.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_unsameq, organization={Wolfram Research}, title={UnsameQ}, year={1991}, url={https://reference.wolfram.com/language/ref/UnsameQ.html}, note=[Accessed: 22-November-2024 ]}