WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

"MultidimensionalScaling" (Machine Learning Method)

Details & Suboptions

  • "MultidimensionalScaling" is a nonlinear distance-based dimensionality reduction method. The method attempts to find a low-dimensional embedding of data using a transformation that preserves the pairwise distances.
  • "MultidimensionalScaling" is able to learn nonlinear manifolds; however, it can be slow when the number of examples is large.
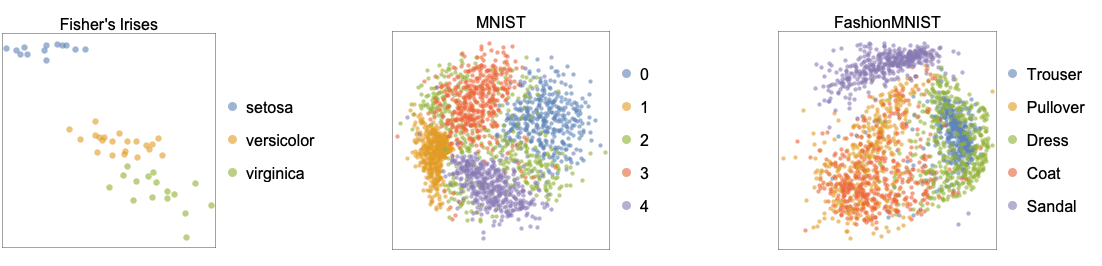
  • The following plots show two-dimensional embeddings learned by the "MultidimensionalScaling" method applied to the benchmarking datasets Fisher's Irises, MNIST and FashionMNIST:
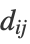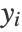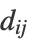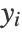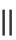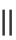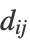  • Given the distance matrix d_(ij) of data points in the original space, "MultidimensionalScaling" attempts to find the lower-dimensional embeddings , such that distances in the lower-dimensional space match the distances between data points in the original space, ||yi-yj||≈ d_(ij). The lower-dimensional embeddings are computed by minimizing the embedding cost: ∑i,j [||yi-yj||- d_(ij)]2.
  • The following suboptions can be given:
  • MaxIterations Automaticmaximum number of optimization steps
    "MinRelativeChange"Automaticminimum relative change of the cost value to continue the optimization process

Examples

open allclose all

Basic Examples  (2)Summary of the most common use cases

Reduce the dimension of random vectors using the "MultidimensionalScaling" method:

In[1]:=1
✖
https://wolfram.com/xid/0fcu9cribt9h07oxaro-b9tmml
Out[1]=1

Create and visualize a "Swiss roll" dataset:

In[1]:=1
✖
https://wolfram.com/xid/0fcu9cribt9h07oxaro-fqjqny
In[2]:=2
✖
https://wolfram.com/xid/0fcu9cribt9h07oxaro-7bpljt
Out[2]=2

Train a nonlinear dimension reducer using "MultidimensionalScaling" on the dataset to map to two-dimensional space:

In[3]:=3
✖
https://wolfram.com/xid/0fcu9cribt9h07oxaro-4b74ci
Out[3]=3

Find and visualize the data coordinates in the reduced space:

In[4]:=4
✖
https://wolfram.com/xid/0fcu9cribt9h07oxaro-hxupzm
Out[4]=4

Visualize the dataset in the original space, with each point colored according to its reduced variable:

In[5]:=5
✖
https://wolfram.com/xid/0fcu9cribt9h07oxaro-2lgnr6
Out[5]=5

Scope  (1)Survey of the scope of standard use cases

Dataset Visualization  (1)

Load the Fisher Iris dataset from ExampleData:

In[1]:=1
✖
https://wolfram.com/xid/0fcu9cribt9h07oxaro-i0qojo
In[2]:=2
✖
https://wolfram.com/xid/0fcu9cribt9h07oxaro-ljl8f4
Out[2]=2

Generate a reducer function using "MultidimensionalScaling" with the features of each example:

In[3]:=3
✖
https://wolfram.com/xid/0fcu9cribt9h07oxaro-hw72bx
Out[3]=3

Group the examples by their species:

In[4]:=4
✖
https://wolfram.com/xid/0fcu9cribt9h07oxaro-u41y3o

Reduce the dimension of the features:

In[5]:=5
✖
https://wolfram.com/xid/0fcu9cribt9h07oxaro-2geip6

Visualize the reduced dataset:

In[6]:=6
✖
https://wolfram.com/xid/0fcu9cribt9h07oxaro-ck8dgi
Out[6]=6

Options  (1)Common values & functionality for each option

MaxIterations  (1)

Load the "MNIST" dataset:

In[1]:=1
✖
https://wolfram.com/xid/0fcu9cribt9h07oxaro-tcwdw7

Reduce the dimension of images using "MultidimensionalScaling":

In[2]:=2
✖
https://wolfram.com/xid/0fcu9cribt9h07oxaro-51nrd6

Find the reduced features using a different MaxIterations option:

In[3]:=3
✖
https://wolfram.com/xid/0fcu9cribt9h07oxaro-o6o2zn

Visualize the obtained features and compare the results:

In[4]:=4
✖
https://wolfram.com/xid/0fcu9cribt9h07oxaro-5vrs5c
Out[4]=4