名前付き群

Wolfram言語は多数の重要な有限群に対する置換表現を提供している．これらの群の中には無限族に属し，1つ以上の整数によりパラメータ化されているものもあれば，その特性により一意に区別されるものもある．後者はその発見者の名前が付けられることが多い．

以下は10次の交代群である：

位数を計算する：

明示的な置換表現の生成元を与える：

これらの生成元から，明示的に群を再構築することができる：

Wolfram言語は次の無限群族およびパラメータ化された族に属さないいくつかの群に関する情報を提供する．

SymmetricGroup[n]	次数 n の対称群
AlternatingGroup[n]	次数 n の交代群
CyclicGroup[n]	次数 n の巡回群
DihedralGroup[n]	次数2n の n 面体の二面体群
AbelianGroup[{n₁,n₂,…}]	いくつかの巡回群の直積と同型のアーベル群

名前付きの無限群族

マシュー(Mathieu)群

次の5つのマシュー群は，19世紀後半に発見された最初の5つの散在型単純群である．これらはすべて多重可移群であり，最大の群の部分群となっている．Wolfram言語はそれらに対してデフォルトの置換表現を提供する．

MathieuGroupM11	11個の点に作用する第1のマシュー群M11
MathieuGroupM12	12個の点に作用する第2のマシュー群M12
MathieuGroupM22	22個の点に作用する第3のマシュー群M22
MathieuGroupM23	23個の点に作用する第4のマシュー群M23
MathieuGroupM24	24個の点に作用する第5のマシュー群M24

マシュー群

これらは，5つの散在型単純マシュー群の位数である：

24個の点に作用するMathieuGroupM24の置換表現の明示的な生成元：

MathieuGroupM24が5次可移群であることを示すために，群自体の推移性とその群の最初の4つの固定部分群の推移性を調べる：

しかし，5つの点からなる固定部分群は，その動作が2つの非自明な軌道に分割されるために推移的ではない：

次は群における基底の点の固定部分群の位数である．これらは群MathieuGroupM24，MathieuGroupM23，MathieuGroupM22に対応しており，さらにマシュー群

，マシュー群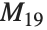

とも呼ばれることのある後3つの群に対応している．後者3つは単純群ではない．また，位数3の巡回群，および自明群がある：

MathieuGroupM12で始まる同様の鎖が得られる．これにはMathieuGroupM11の他，マシュー群M10，マシュー群M9，マシュー群M8と呼ばれる非単純群，そして最後の自明群が含まれる：

MathieuGroupM24の最大の置換位数は23であることが知られている．次が例である：

他の散在型単純群

散在型単純群は26個（ティッツ群を含めると27個）ある．5つのマシュー群以外に，Wolfram言語は台の長さが中程度の群に対する置換表現を提供する．最大のものは実際に置換群として扱うには大きすぎるため，そのようなものは行列群として表した方が効率的である．次は5万個の点より少ない領域上での表現が知られている13の群（ティッツ群を含む）である．

HigmanSimsGroupHS	Higman–Simsの散在型単純群
McLaughlinGroupMcL	McLaughlinの散在型単純群
JankoGroupJ1	Jankoの散在型単純群
JankoGroupJ2	Jankoの散在型単純群
JankoGroupJ3	Jankoの散在型単純群
ConwayGroupCo2	Conwayの散在型単純群
ConwayGroupCo3	Conwayの散在型単純群
SuzukiGroupSuz	Suzukiの散在型単純群
HeldGroupHe	Heldの散在型単純群
RudvalisGroupRu	Rudvalisの散在型単純群
FischerGroupFi22	Fischerの散在型単純群
FischerGroupFi23	Fischerの散在型単純群
TitsGroupT	Titsの単純群

中間の散在型単純群

散在群の中には，24次元ユークリッド空間における特別な格子であるリーチ格子の対称性に関連したものがある．これらは，場合によっては散在型単純群の第2世代とも呼ばれる．

第2世代の6つの群である：

その位数は以下の通りである：

次は提供されている表現の置換次数である：

例えば，以下は100個の点に作用するJankoGroupJ2の生成元である：

これは群の中の最後の置換である：

写像に対応するリストである：

次は2300個の点に作用するConwayGroupCo2の固定部分群の鎖である．基底には6個の点しかないので，これら6個の点のイメージを知っているだけで群の中のそれぞれの置換を一意的に見付けるのに十分である：

次は5万個未満の点で置換群として表すことのできる他の散在型単純群である：

その位数と次数は次の通りである：

ONanGroupON	O'Nanの散在型単純群
HaradaNortonGroupHN	原田–ノートンの散在型単純群
ConwayGroupCo1	Conwayの散在型単純群
FischerGroupFi24Prime	Fischerの散在型単純群
ThompsonGroupTh	Thompsonの散在型単純群
JankoGroupJ4	Jankoの散在型単純群
LyonsGroupLy	Lyonsの散在型単純群
BabyMonsterGroupB	Baby monster散在型単純群
MonsterGroupM	Monster単純群