已命名的群

Wolfram 语言对许多重要的有限群提供置换表示. 其中有些是无限族的成员，被一个或多个整数参数化；其它群按它们特殊的属性被单独区分，且经常以它们的发现者来命名.

10次交错群：

计算阶数：

给出显式置换表示的生成元：

从这些生成元中，可以重新显式构建群：

Wolfram 语言为以下群的无限族以及一些不属于参数化系列的群提供信息.

已命名的群的无限族.

以下5个 Mathieu 群是5个在19世纪的下半叶首先被发现的散在单群，它们都是多重传递群而且均是最大群的子群. Wolfram 语言为它们提供默认的置换表示.

Mathieu 群.

以下是5个散在 Mathieu 单群的阶数：

作用于24个点的 MathieuGroupM24 置换表示的显式生成元：

为了显示 MathieuGroupM24 是5可递的，验证群自身以及其首四个稳定子群的传递性：

然而，5点的稳定子群不是可传递的，因为其作用分成两个非平凡的轨道：

以下是群中一个基的点的稳定子群的阶数. 它们对应与群 MathieuGroupM24、MathieuGroupM23、MathieuGroupM22，以及其它三个群，有时称为Mathieu 群

、Mathieu 群

、以及 Mathieu 群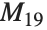

，但并不是单群. 最后是阶数为3的循环群和平凡群：

一个类似的链可以从 MathieuGroupM12 中获得. 其包含 MathieuGroupM11 以及非单群，Mathieu 群

，Mathieu 群

以及 Mathieu 群

，最后是平凡群：

已经发现，MathieuGroupM24 中最大的置换阶数是 23. 以下是一个例子：

有26个散在单群（如果包括 Tits 群则有27个）. 除了5个 Mathieu 群，Wolfram 语言对于那些中等支撑长度的群提供置换表示. 最大的因为太大了而实际中不能以置换群来处理，而以矩阵群表示则更有效. 以下是13个群（包括 Tits 群），它们在少于50000个点的域中表示是已知的.

中等散在单群.

一些散在群与 Leech 点格的对称性相关，它是欧几里德（Euclidean）24维空间的一个特殊点格. 这些群有时被称为“第二代”散在单群.

第二代的六个群：

它们的群阶数为：

以下是提供的表示式的置换次数：

例如，作用于100个点的 JankoGroupJ2 的生成元：

这是群中最后的一个置换：

这是它的相应的像的列表：

这是作用于2300个点的 ConwayGroupCo2 的稳定子群的链. 其基只有6个点，因此，只要知道这6个点的像就足以唯一确定群中的每个置换：

以下是在少于50000个点上可用置换群表示的其它散在单群：

它们的阶数和次数显示如下：