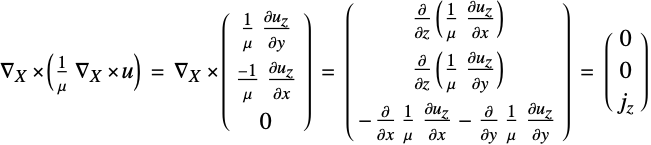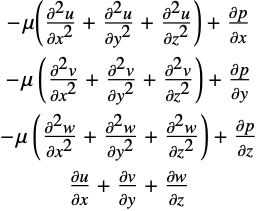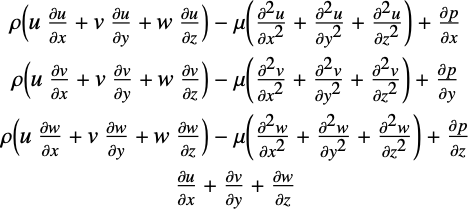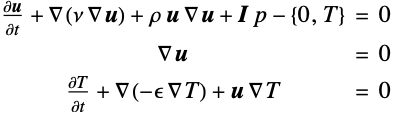有限要素法で偏微分方程式を解く
はじめに
このチュートリアルは，有限要素法(FEM)の概要を，NDSolveに実装されているように，紹介するものである．ノートブックは，偏微分方程式を解くための有限要素法の概念を紹介する．まず，典型的なワークフローについて説明する．領域，境界条件，方程式の設定の後には，NDSolveを使った偏微分方程式の解法について述べる．その後，解の可視化とアニメーション化を紹介し，有限要素法の理論的な部分について提示する．ポアソン(Poisson)方程式や熱方程式といった標準的な偏微分方程式についても説明する．また，結合偏微分方程式についても構造力学および流体動力学の例とともに紹介する．
なぜ有限要素なのか
偏微分方程式で明示的な閉形式の解が得られることはほとんどない．有限要素法は，偏微分方程式を数値的に解く方法である．これは，最低でも2つの理由から重要である．まず，有限要素法は，偏微分方程式をほとんどどのような形の領域においてでも解くことができる．さらに，この方法は，いろいろな種類の偏微分方程式に使うのに適している．特定の領域上の特定の偏微分方程式を解くのに，よりよい方法を見付けることは，ほとんどの場合可能であるが，有限要素法は，広範囲の偏微分方程式に対して使用することができる．つまり，有限要素法は，以下を取り扱えるという点で重要である：
有限要素の分析に必要なもの
偏微分方程式を有限要素法を使って解くには，次の3つが必要である：
このセクションでは，偏微分方程式とその境界条件について見ていく．有限要素メッシュは，ToElementMeshで生成することができる．有限要素メッシュの生成についての詳しい説明は，「要素メッシュの生成」をご覧いただきたい．
NDSolveに実装される有限要素法のスコープ
有限要素法の実装の現行バージョンでは，以下の機能をサポートする：
以下のセクションでは，この機能の概要を提供する．特定の物理や工学の分野において，どのような偏微分方程式が解けるかについての詳しいリストは，「PDE Modelsの概要」ページおよびガイドページ「偏微分方程式項」も参照されたい．
領域
有限要素の分析を行うためには，偏微分方程式を解く領域を定義しなければならない．空間独立変数のそれぞれについて，{v,vmin,vmax}を使って矩形領域を指定することができる．厳密な引数の指定については，NDSolveValueに詳細がある．
表記 vars∈Ωを使って任意の形の領域を指定することができる．ここでΩは，RegionQ[Ω]がTrueを返す領域である．
矩形領域ではない領域を指定する1つの方法に，ブール述部を使う方法がある．述部は，TrueあるいはFalseを返す関数である．「述部」という用語には数学的にいろいろな意味があるので，「ブール述部」 という用語を使い，この述部がブールを返すことを強調する．領域を表すために，ブール述部を例えばRegionPlotおよびRegionPlot3Dのような関数に使うことができる．
このチュートリアルでは，領域やメッシュの作成については強調せず，有限要素法を使って偏微分方程式を解くことに焦点を当てる．このことについての詳細は，「要素メッシュの生成」をご覧いただきたい．
古典的な偏微分方程式
偏微分方程式の係数形式
NDSolveに実装されるように，有限要素法を使ってどのような方程式を解くことが可能であろうか．
での単一の偏微分方程式を考える．
偏微分方程式は
で定義される．ここで 
は，解が求められる従属変数である．係数 
，
，
，
はスカラー，
，
，
はベクトル，
は 
×
行列である．
次に挙げるのは，よく知られている偏微分方程式のいくつかと，その対応する係数である．(1)の一般性を示すために，特定の方程式に関係のある部分は赤で，関係のない部分は灰色で示す．
ラプラス(Laplace)方程式には，拡散項が含まれるだけである．
ポアソン(Poisson)の方程式をモデル化するには，少し変更し，負荷項 
を加えるだけでよい．
ヘルムホルツ(Helmholtz)の方程式には，反応項 
を加える．
対流・拡散・反応のタイプの方程式もよく使われる偏微分方程式である．上の例と比べると，これらには，追加の対流項 
が含まれる．
ここまで見てきた偏微分方程式は，定常である．つまり，時間に依存しない．熱方程式は，ポアソン方程式に時間依存を加えたものであり，以下の形式を持つ．
方程式(1)は，次数2までの空間導関数を提供するので，広範囲に渡るさまざまな現象をモデル化するためのコンポーネントを提供する．
ディリクレ(Dirichlet)条件のポアソン(Poisson)方程式
ポアソン方程式は，ディリクレ境界条件を使って，領域
上で解かれる．まず，方程式を解く領域を定義しなければならない．それから，方程式と境界条件が定義される．最後に方程式がその領域上で解かれる．
第3のステップとして，境界条件を設定する．最初のディリクレ境界条件は，x0∧8≤y≤10の評価が領域
の境界上でTrueを返す場合には必ず，従属変数 
を0の値に強制する．この場合，これは境界の左上部分である．2つ目のディリクレ境界条件は，
が領域
の境界上でTrueを返す場合には必ず，従属変数 
の値を指定する．境界条件については，後のセクションで詳しく説明する．
解のステップでは，NDSolveは偏微分方程式，境界条件，領域を必要とする．
内部では，領域
は有限要素メッシュに変換され，有限要素法が自動的に方程式を解くのに使われる．
偏微分方程式と境界条件
NDSolveおよびその関連の関数では，ディリクレ条件，ノイマン値，周期境界条件という3種類の空間境界条件を指定することができる．
ディリクレ境界条件は，境界の一部における値 
の従属変数 
上で条件を指示する．
一般化されたノイマン境界値（ロビン(Robin)値としても知られる）は，値 
を指定する．値 
は，境界の部分上の外向きの法線での流束を指示する．
有限要素法は，微分方程式の弱形式に基づく．この形式は，方程式(1)を取り，これにいわゆるテスト関数 
を掛け，領域
上で積分することによって得られる．
この過程は，内部的に行われる．(11)内の境界積分の被積分関数 
は，
(9) で置換され，以下を返す．
は，弱形式の境界積分の被積分関数(11)の値を指定するので，NeumannValueという名前を持つ．
部分ごとに積分を行って方程式(11)を得る代りに，発散定理とグリーンの恒等式を使うこともできる．
周期境界条件は，従属変数を，境界の2つの独立した部分間に与えらる関係に従って動作させる．ほかの境界条件もあり得るが，現在のところは実装されていない．
ほとんどの場合，ディリクレ境界条件は，特定の方程式に関連付けられている必要はなく，方程式とは独立して指定することができる．ディリクレ境界条件は方程式として指定される．一般化されたノイマン値は，それに対して，値を与えることで指定される．満たされる方程式が値では陰的であるからである．ノイマン値は，数学的に偏微分方程式に結び付けられている．
実用的な理由から，NDSolveおよび関連関数NeumannValueは，方程式の一部として与えられなければならない．結合偏微分方程式系を考えてみよう．その偏微分方程式系のどの指定の単一偏微分方程式に対してでも任意の与えられたノイマン値を明瞭的に指定できると望ましい．偏微分方程式の値が関連付けられているノイマン値から，これを（明瞭的に）導き出すことは不可能である．偏微分方程式のNeumannValue部分を作ることで，明瞭にこの問題を解決できる．偏微分方程式内でDirichletConditionを与えることもできる．
| {op[u[x1,…]] ΓN,ΓD,ΓP} | 微分演算子 op，ノイマン境界値ΓN，ディリクレ境界条件方程式 ΓDおよび周期境界条件ΓPを持つ偏微分方程式 |
| {op1[u[x1,…],v[x1,…],…] ΓN1,op2[u[x1,…],v[x1,…],…] ΓN2,…,ΓD,ΓP} | 結合偏微分方程式の演算子 opj，ノイマン境界値ΓNj，ディリクレと周期の境界条件の方程式ΓDとΓPの系 |
DirichletCondition，NeumannValue，PeriodicBoundaryConditionはどれも，第2引数として，条件または値が適用される境界上の位置を示す述部が必要である．さらに，PeriodicBoundaryConditionは，境界の2つの部分間の関係を指定する第3引数を持つ．
偏微分方程式は通常，領域のある部分について，一意的に解ける少なくとも1つのディリクレ境界条件が必要である．このため，ディリクレ境界条件は，必須の境界条件とも呼ばれる．
一般化されたノイマン値は，弱形式の積分形式から使用されることになるので，通常自然条件とも呼ばれる．
純粋なノイマン境界方程式は，
である一般化されたノイマン境界方程式(9)である．
も指定されない場合には，ノイマンのゼロ境界値が自動的に示唆される(
)．
そうすると，ノイマン値はゼロであり，項が(12)では削除される．これは，境界に流束や応力がない場合に通常起る．領域境界 
の一部に対して境界条件が明示的に指定されていない場合には，ノイマンのゼロ値が想定される．
ノイマン(Neumann)値のポアソン(Poisson)方程式
一般化されたノイマン境界値で，ポアソン方程式を解くことを考えてみよう．
ノイマンタイプの方程式の正規導関数がどのように偏微分方程式に関連付けられているかに注意されたい．ノイマン境界方程式では，右辺の 
と 
の値を指定する．左辺は，偏微分方程式を通して暗黙的に指定されている．偏微分方程式の係数 
が恒等行列として与えられている場合には，ノイマン条件の左辺の係数 
は，その同じ係数 
である．
ノイマン境界値は，値 
と 
を通して指定される．通常，
である場合にはノイマン境界値を使い，
である場合には，一般化されたノイマン境界値，つまりロビン境界値を使う．一般化されたノイマンとノイマン境界値の両方をノイマン境界条件と呼ぶことも多い．
ノイマン境界方程式の項 
内の定数が，偏微分方程式(11)の弱形式からの
内の定数と厳密にマッチすることを確かめることが重要である．これらの項はマッチしなければならないので，NeumannValueでは，境界方程式の右辺だけを入力すればよい．例えば，境界方程式 
を入力する場合には，NeumannValue[1,…]と入力するだけで十分である．境界方程式の左辺の正しい式（つまり 
）は，偏微分方程式(12)の弱形式における項 
によって示唆される．ノイマン境界値と偏微分方程式の間のこの密接な関係は，方程式のNeumannValue部分を作成することによって，さらに対応することができる．
前の例では，すべての境界に境界条件が明示的に指定されてはいなかった．それらの部分の境界については，ノイマンのゼロ条件が使われる．
ディリクレ条件で必要とされるように，8を超える値はゼロであることに注意する．
周期境界条件を持つポアソン方程式
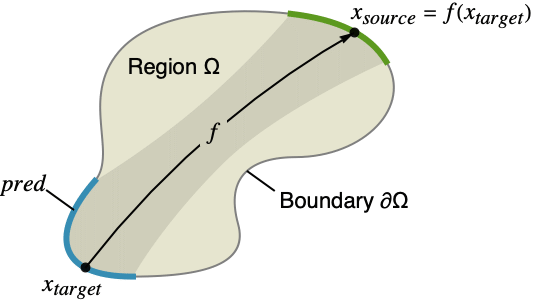
PeriodicBoundaryConditionは，境界の2つの独立した部分における偏微分方程式の解の値を関連付けるためのものである．PeriodicBoundaryCondition[a+b u,pred,f]は，解が独立したソースからの値に関連付けられるべきである点におけるターゲットを述部 pred が指し，関数 f がターゲット位置（青）から，従属変数関係が評価されるソース位置（緑）までの座標をマップする周期境界条件を指定する．結果の値は，ターゲットにおける条件として設定される．
PeriodicBoundaryConditionがどのように動作するのかを理解するのには，例を見るのが最もよい方法である．
この例では，偏微分方程式は，
で指定される長方形内で1単位の負荷項がアクティブであるラプラシアンである．それ以外の場所では，負荷は0である．
PeriodicBoundaryConditionを使うと，周期境界条件，反周期境界条件，関係境界条件のいずれかをモデル化することができる．この例では，周期境界条件が示されている．周期条件は，第1引数が従属変数 u であり，この従属変数 u が述部 
（青，ターゲット）が位置
（緑，ソース）においてと同じ値を持つようにしなければならない場合に指定される．解を求める過程で，この従属変数 u は，ソースにおいて評価される．このため，述部 
（青，ターゲット）から
（緑，ソース）へのマッピングが必要となる．関数FindGeometricTransformは，座標のリストからそのようなマッピングを構築することができる．
マッピングが緑色のソースから青色のターゲットまでの点をマップするかどうかを調べる．
その後，従属変数，ターゲット述部，マッピングの関係を与えることによって，PeriodicBoundaryConditionを設定する．周期条件の場合は，関係は 
である．
さらに，両方の曲線の辺に，DirichletConditionが置かれる．DirichletConditionは，ターゲットの境界上にDirichletConditionがないように，
では除外されることに注意する．そこにディリクレ境界条件があると，それらの場所にマップされた解と整合性がなくなってしまう．
反周期境界条件は，PeriodicBoundaryConditionにおける従属変数の負を使うことにより実現できる．次の例では，反周期境界条件以外はすべて上と同じである．
変数係数を持つ偏微分方程式
次の例では，偏微分方程式の係数は空間と時間に従属する．ここでは，
は時間変数を， 
は空間変数を示す．
遮断されたマイクロストリップの例は，変数係数の効果を示す． これは，ポアソン方程式でモデルできる静電学の応用である．この方程式では，係数 
が相対誘電率 
であり，空間に依存する．
ここで，境界が2つの物質を分離する形状を構築する．それぞれの物質において，
は異なる値を持つ．
まず，境界メッシュが作成される．要素メッシュの作成についての詳細は，ToBoundaryMeshを参照いただきたい．
境界メッシュから要素メッシュへの変換は，ToElementMeshを使って行う．
次に偏微分方程式を設定する．偏微分方程式の負荷項 
は，電荷密度 
を真空誘電率 
で割ったものである．
形状 
の下の部分はシリコンであり，上の部分は真空である．シリコンの相対誘電率は約11.7であり，真空の値は1である．
効率的な計算が行える偏微分方程式係数を設定する方法については，このチュートリアルも参照されたい．
偏微分方程式でInactiveを使うことについては，形式的な偏微分方程式のセクションを参照のこと．
ポテンシャル 
は，
である場合には必ず0に設定される．2つ目のポテンシャルは，内側のストリップで1000に設定される．
偏微分方程式係数に明示的な不連続性がある場合には，NDSolveが生成するメッシュにこれらの不連続性を自動的に含むことによって，問題を解決することが多い．
における不連続性は，この例では自動的に検知される．
見て明らかなように，もとの入力領域 
は不連続性に対して何も示さないが，メッシュ生成過程中に，不連続性に沿って内部に線が加えられている．
複数のものをモデリングする代りに，特定の領域部分にマーカーを使うこともできる．この方法については，「要素メッシュの生成」の「マーカー」セクションに詳しく説明されている．
その他にも，複数マテリアルの応用例が数多く「PDE Modelsの概要」ページに掲載されている．
また，効率的な偏微分方程式係数の設定についてのこの説明も参照されたい．
非線形係数を持つ偏微分方程式
偏微分方程式の係数の中には，空間 
および時間 
に加えて，従属変数 
および一次導関数 
に依存するものもある．ここでは，
は空間変数 
, 
, 
を指す．係数が従属変数 
に依存する場合には，その方程式は非線形である．以下の非線形方程式を見てみよう．
従属変数の導関数が拡散係数内に現れるので，この方程式は非線形である．
非線形の定常方程式を解くために，解の初期シード値が指定する．これは，InitialSeedingsを使って行う．InitialSeedingsは，興味領域上で評価する式を指定する．この式は空間変数に依存することができる．初期シード値が指定されていない場合には，初期シード値は0であると想定される．
InitialSeedingの使用例は関数ページにも掲載されている．
その他にも，非線形の応用例が数多く「PDE Modelsの概要」ページに掲載されている．
非線形の変数係数を持つ偏微分方程式
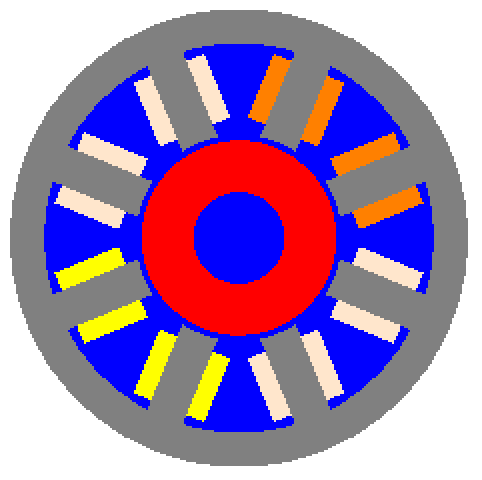
以下のセクションでは，静磁場のアプリケーション例を示す．静磁場のアプリケーションでは通常シミュレーション範囲のさまざまな部分において，いくつかのマテリアル（非線形も可能）を利用する．この例では，磁位の分布と磁束のベクトル密度場が計算することで，モーターの簡単なモデルを見てみる．
上に表されるモーター形状では，固定子セクションが灰色，回転子が赤で表され，青い部分は空気を表している．またいくつかのコイルがグループになっていて，それぞれオレンジ色，薄いオレンジ色，黄色で表されている．
偏微分方程式モデルは，マクスウェル方程式のアンペールの法則から導き出されたものである．
ここで 
は電流密度，
は透磁性である．磁束密度 
iは，磁位 
に以下を通して接続されている．
電流が 
平面と 
平面に直角にだけ流れると仮定して，モデルを2次元に簡約化し，
を得る．さらに 
が 
方向に一定で，
と 
が一定であると仮定すると，以下のように書くことができる．
モデルは 
方向に均一であると仮定されるので，
部分を無視して，以下を使うことができる．
透磁性 
は空間座標 
と未知の導関数 
の関数であるので，方程式は非線形である．固定子と回転子では強磁性物質の透磁性が使われるのに対し，残りの領域では，空気の透磁性が使われる．方程式の右辺 
は，コイルを流れる変数電流密度の 
成分である．
まず最初にさまざまな範囲に対してマーカーがあるメッシュを作成する．これらのマーカーはその後，例えばシミュレーション範囲のさまざまな領域で 
をアクティベートするのに使うことができる．マーカーを使うこの方法は，偏微分方程式のさまざまな部分がアクティブである場合に領域について公式をしていするよりもずっと簡単である．マーカーとメッシュでのマーカーの生成についての詳細は，「要素メッシュの生成」のチュートリアルで説明されている．
マーカーがさまざまな部分領域に起因するものとするには，これらの部分領域にある座標を指定しなければならない．
境界メッシュとマーカー座標を可視化すると，マーカー座標を指定する過程が理解しやすくなる．可視化のためには，マーカー座標をグループ化して，マーカーに使う色を設定しなければならない．
オレンジの点で可視化されているコイルは，さまざまな電流を伝導する．この過程を簡約化するために，同じ電流が流れるコイルを一緒のグループにするように，それぞれのコイルにマーカーが割り当てられる．
これで部分領域にある座標のリストが得られ，これらの座標にマーカーが割り当てられる．
強磁性物質の透磁性は通常磁化（B-H）曲線で与えられる．これらの曲線には物質データが含まれる．このデータについて，偏微分方程式の係数として使える補間関数が作成される．より効率的な方法として，偏微分方程式の係数として使えるフィットが生成できる．両方の方法を以下に示す．
補間関数が領域外でクエリされた場合には，補間を生成している間に，磁化曲線の最小値と最大値が継続するようにしなければならない．また，領域外でクエリを行う場合に補間関数が警告メッセージを発しないように指示しなければならない．
透磁性係数が固定子または回転子で評価される場合には，空気の透磁性が使われるすべてのその他の領域で強磁性物質が使われる．
補間関数の方法は非常に柔軟なので，係数 
がそのまま使える．しかし，より効率的に評価できる方法は，磁化曲線データのフィットを求める方法である．
効率的な計算が行える偏微分方程式係数を設定する方法については，このチュートリアルも参照されたい．
コイルの電流密度は，ElementMarker 4の要素内には正電流，ElementMarker 6の要素内には負電流，それ以外の場所には零電流が流れるように指定する．
固定子の外側の端において磁位がゼロであるように，境界条件を設定する．
InitialSeedingの使用例は関数ページにも掲載されている．
その他にも，非線形の応用例が数多く「PDE Modelsの概要」ページに掲載されている．
偏微分方程式と非線形境界条件
NDSolveおよび関連する関数では，非線形の一般化されたノイマン値を指定することができる．ディリクレ境界条件と周期境界条件は非線形にはならない．非線形の一般化されたノイマン値は以下で与えられる．
これは，線形の一般化されたノイマン値に非常によく似ているが，従属変数 
が 
の関数である点だけ異なる．
非線形の一般化されたノイマン値がよく使われるのは，放射境界をモデル化する際である．一次元の例として，非線形の放射熱移動が使われる．
左辺の境界では，ディリクレ条件を利用する．ここで，
は熱移動率係数，
は放射にさらされた横断面積，
はシュテファン・ボルツマン（Stefan–Boltzmann）定数，
は放射率，
は周囲温度，
は熱源である．
類似の例を確かめるためには， 「非線形有限法の検証テスト」を参照されたい．
熱方程式
ディリクレ境界条件もノイマン境界値も時間に依存することがある．
偏微分方程式を解く全体的な手順は同じである．領域を指定し，境界条件を持つ偏微分方程式を設定しなければならない．
一階の時間依存問題を解くには，NDSolveは初期条件と時間領域が必要である．
メッシュを一度変換し，離散化されたメッシュをプロット中に使用する方が，各アニメーションフレームについて領域を再度離散化するよりも，効率的であることに注意されたい．
熱移動方程式と適用可能な境界条件についての情報は，「熱移動」のチュートリアルと「熱移動の偏微分方程式と境界条件」のガイドページに記載されている．
波動方程式
波動方程式は，二階の時間依存偏微分方程式であり，初期条件と初期条件の導関数が指定されなければならない．
結果のInterpolatingFunctionのアニメーションの作成には，Plot3DとAnimateを使う．
境界条件が指定されていない場合（陰的にこれはノイマン零境界条件を意味する）には，波動は境界において反射されている．これは1Dの例でよく見ることができる．
InterpolatingFunctionの結果のアニメーションを作成するためには，Plot3DとAnimateを使う．
時間依存の系には，境界条件は，方程式の従属変数の時間導関数の次数よりも厳密に小さい次数の従属変数の任意時間導関数に対して指定することができる．このため，時間において一次である方程式については，境界条件は従属変数についてだけ与えることができる．時間において二次である方程式については，境界条件は従属変数と，時間についてのその一次導関数に対して与えることができる．
吸収境界条件を持つ波動方程式をモデル化するためには，ノイマン境界条件の時間導関数を使う．これには，上で使われた波動方程式と全く同じものが使われるが，方程式にノイマン値が加えられる．
結果のInterpolatingFunctionのアニメーションを作成するためには，Plot3DとAnimateを使う．
波動の周期境界条件をモデル化することは，PeriodicBoundaryConditionを使って実装することができる．この例では，初期条件の導関数はゼロではないが，初期の波動が右に移動するように選ばれる．
結果のInterpolatingFunctionのアニメーションを作成するためには，Plot3DとAnimateを使う．
形式的な偏微分方程式
上の例では，偏微分方程式はLaplacianを利用して設定されている．そのまったく同じ偏微分方程式は，DivとGradを使って形式化することができる．それを行うには，
で係数 
を使う．ここで 
は，
×
行列（
は
内の次元
の数）である．
Inactiveを使うと，評価をしないようにすることができる．
偏微分方程式の形式的なバージョンでは，係数行列 
を変更することができる．
Inactiveの使用が重要となってくる状況の一つとして，偏微分方程式とノイマン値の関係をモデル化する場合が挙げられる．以下の偏微分方程式を考える．
が恒等行列であり，
が
で与えられる偏微分方程式を考える．Inactiveを使わずに偏微分方程式を指定すると，式が評価される．
ただし，評価によって偏微分方程式が以下のように変化することに注意されたい．
ここで 
は{-e(-x-y),-e(-x-y)}，
は2e(-x-y)である．
評価を妨げ，以下の形式のノイマン値をモデル化するためには，Inactiveを使用することが必要である．
形式的な偏微分方程式についての詳細は， 「有限要素法の使用上のヒント」にある．
また，係数を関数として指定することは可能であるが，これを行うと，内部コードが係数積分を最適化することができなくなることに注意する．ここでは，係数は定数であり，最適化で係数は一度だけ積分される．ブラックボックス関数は，領域上で継続的に評価することが必要である．例えば，有限要素法のコードが最適化された拡散演算子を定数の係数に使うことができないので，内部を隠す関数は理想的ではない．
偏微分方程式系
偏微分方程式系の係数形式
内の領域
については，各 
は，
×
行列であり，
，
，
のそれぞれはベクトルである．
一次元の結合偏微分方程式
次の例は，パラメータが簡単に変更できるように設定されている．まず，領域
を指定する．
偏微分方程式には，2つの従属変数 
と 
がある．結合は，2つの拡散演算子間である．これは一次元の系であるので，それぞれの 
係数は1×1の行列であり，これは数に等しい．
それぞれの方程式は，独自の境界条件を持つ．最も一般的な形式では，ディリクレ境界条件は条件の系である．
現行の実装は，ディリクレ条件の交差結合はサポートされていない．
と 
の項は与えることができない．
以下は，DSolveを使って計算された，偏微分方程式の系の解析的な解である．
方程式系のDSolve形成において，一般化されたノイマン境界方程式がどのように明示的に与えられなければならないか，およびそれらの係数がどのように偏微分方程式の係数にマッチしているかについて注意する．
解析的な結果を数値結果と比べるために，2つの差分のプロットを作成する．
この例によって，なぜNeumannValueが方程式の一部であるのかも明らかになる．ノイマン値の方程式は以下で与えられる．
ノイマン値からは，どの方程式に関連付けられるべきであるかは分からない．ノイマン値を方程式の一部とすることによって，どれにノイマン値が関連付けられているかが明らかになる．
構造力学
構造力学では，負荷をかけられたときのオブジェクトの変形が計算される．構造力学は，よい結合偏微分方程式の例を提供する．領域の例として，5単位の長さで1単位の高さを持つ梁を考える．
物理をモデル化する偏微分方程式は，平面応力関係であり，薄いオブジェクトに有効である．ここで，「薄い」とは，オブジェクトの他の寸法に比べて薄いことを意味する．平面応力形成は，2つの従属変数と1つの独立変数に依存する．2つの従属変数は，変形したオブジェクトの成分規模での寄与を与える．物質データとして，ヤング(Young)の係数 
とポアソン率 
が指定されなければならない．
演算子は，Inactive形式の形式的な偏微分方程式として与えられる．
あるいは，関数SolidMechanicsPDEComponentを使って偏微分方程式成分を生成することもできる．SolidMechanicsPDEComponentの関数ページにもテキスト形式の方程式が含まれている．
さらに，境界負荷も指定されることがある．この場合は，境界負荷は梁の右端に加えられ，
単位の圧力が負の 
方向に加えられる．
領域の左側では，どちらの従属変数も0の変位で固定されている．
変形した梁を示すためには，静止している梁について要素メッシュを作成しなければならない．この梁は，与えられた補間関数によって変形される．
ElementMeshDeformationの使用についての詳細は，「要素メッシュの可視化」 を参照されたい．
以下の等高線プロットは，梁の変形を示す．従属変数 
は，
方向の変形を表す．梁の右上部分において，正の 
方向にシフトしたことが分かる．右下の部分は負の 
方向に動く．
従属変数 
の等高線プロットは，
方向の変形を表す．梁の右側は，負の 
方向に変形する．
ここで，2つの等高線プロットの色スケールが同じではないことに注意する．
分析を完全なものにするため，物理の平面ひずみをモデル化する偏微分方程式を提示する．平面ひずみの形成は，平面応力の形成とは対照的に，太いオブジェクトに有効である．ここで「太い」とは，オブジェクトの他の寸法に比べて太いことを意味する．平面ひずみの形成は，2つの従属変数と独立変数に依存する．2つの従属変数は，変形したオブジェクトの成分規模での寄与を与える．物質データとして，ヤング(Young)の係数 
とポアソン率 
が指定されなければならない．
ここでも，成分は関数SolidMechanicsPDEComponentを使って生成されている．
この場合の境界条件は，両側への指定された変位である．領域の左側では，どちらの従属変数も0の変位で固定されている．右側では，負の 
軸の方向に，1単位の変位が与えられ，
方向の変位は固定されている．
変形した梁を示すためには，静止している梁について要素メッシュを作成しなければならない．この梁は，与えられた補間関数によって変形される．
以下の等高線プロットは，梁の追加的な変形を示す．従属変数 
は 
方向の変形を，従属変数 
は 
方向の変形を表す．
固体力学と適用可能な境界条件についての詳細は，「固体力学」のモノグラフおよび「固体力学の偏微分方程式と境界条件」のガイドページに記載されている．
液体の流れ
液体の流れの線形モデルは，ストークス方程式である．三次元のストークス方程式を以下に挙げる．
ここで 
，
，
はそれぞれ，
，
，
方向の液体の速度である．
は圧力，
は液体の動的粘度である．
この例では，狭まっている二次元の管を通る流れについて分析する．
演算子は，Inactive形式の形式的な偏微分方程式として与えられる．
ここでは，
は 
方向の液体の粘性を，
は 
方向の粘性を表す． 
は液体内の圧力を示す．
方向の流入の粘性を境界条件を使って規定する．これは，領域左側の 
の従属変数についての流入の輪郭を指定することによって可能である．領域の底と上の部分では，流れの条件は指定されない．これは，これらの部分の 
と 
の成分を0に設定することによって可能である．流出条件は，領域の右側で設定する．ここでは，圧力 
は，任意に0と設定する．一般に，それぞれの従属変数はディリクレ条件またはロビン型のノイマンが指定されているべきである．ノイマン0のような純粋なノイマン値では不十分である．その場合，方程式の解は定数までのみ正しい．
粘性が圧力よりも高次で補間される場合には，安定した解が求まる．NDSolveを使うと，それぞれの従属変数の補間次数を指定することができる．ほとんどの場合，"InterpolationOrder"を指定する必要はないが，これは液体の流れに有限要素法を使うときには標準的な過程であり，Wolfram言語ではこのように行われる．この設定は，P2P1型あるいはQ2Q1型の要素と呼ばれるものに対応しており，これらの要素はTaylor–Hood（テイラー・フード）要素としても知られる．"InterpolationOrder"を使わないと，すべての変数に対して二次補間を使うことになるが，それでもよい．すべての従属変数に対して一次補間を使うと，誤った結果になることがあり，数値的に安定しないかもしれない．速度に二次，圧力に一次を指定すると，解の確度がよくなり，離散化された偏微分方程式モデルのサイズが少し小さくなる．
有限要素法オプションの補間次数の使用については， 「有限要素法の使用上のヒント」で説明されている．
流量の非線形モデルは，ナビエ・ストークス(Navier–Stokes)方程式である．ナビエ・ストークス方程式を以下に挙げる．
この例では，2Dの横断面をチェックすることによって，円柱の周りの流入を分析する．
演算子は，Inactive形式の形式的な偏微分方程式として与えられる．
もう一つの方法として，関数FluidFlowPDEComponentを使ってより一般的に使えるナビエ・ストークス偏微分方程式成分のバージョンを生成することも可能である．FluidFlowPDEComponentの関数ページにはテキスト形式での方程式も含まれている．
ここで 
は液体の 
方向の速度，
は 
方向の速度を表す．
は液体中の圧力を表す．
方向の流入速度は，境界条件で規定される．これは，境界の左側の 
従属変数についての流入統計データを指定して行う．領域の下と上の部分，および円筒の周りでは，流出入なしの条件が指定される．これは，これらの部分における 
と 
のコンポーネントをどちらも0に設定することによって行う．流出条件は領域の右側で設定される．ここでは，圧力 
が任意に0に設定される．
円筒の前の点
と円筒の後ろの点
からの圧力差
を計算したいとする．さらに 再循環の長さ 
を計算する．円筒のけん引力と揚力も考慮しなければならない．
は円筒の端の 
座標，
は再循環領域の端である．よい結果を得るためには，円筒の周りの領域を梨形にして，デフォルトよりも高い確度と精度をメッシュ生成に使う必要がある．
速度が圧力よりも高い次数で補間される場合には，安定した解が求まる．NDSolveでは，それぞれの従属変数の補間次数が指定できる．
有限要素法のオプションの補間次数の使い方については，「有限要素法の使用上のヒント」に説明がある．
予想される圧力差の値は，0.1172と0.1176の間の値である．
予想される再循環の長さの値は，0.0842と0.0852の間の値である．
予想されるけん引力の値は5.57と5.59の間の値であり，揚力の値は0.0104と0.0110の間の値である．
非定常ナビエ・ストークス（Navier–Stokes）方程式を解くこともできる．ベクトル化した方程式を以下に挙げる．
これには，定常の場合と同じ形状が使われる．まず時間依存のナビエ・ストークス方程式を設定する．
左の流入をモデル化したいとして，右の流出の圧力条件を設定し，残りのすべての壁が滑らない境界条件を持つとする。流入境界条件が初期条件と一致するように，時間の経過とともに滑らかに流入を増やすヘルパ関数を作成する．
ナビエ・ストークス方程式は高指数微分代数方程式であるので，効率的に方程式を時間積分するようにオプションが指定される．時間積分器の最大差分次数は，拒絶されるステップ数を最小化するために減らされる．時間依存境界条件は，時間積分をより効率的に行う一定の方程式系を作成するために微分される．最後に，デフォルトメッシュよりも幾分細かいメッシュが使われる．使用するハードウェアによっては，この方程式を解くのに数分かかることもある．
流量と適用可能な境界条件についての詳細は，層流のモノグラフと流量モデルのガイドページに記載されている．
次のステップとして，ナビエ・ストークス方程式を熱方程式と組み合せて，エネルギー輸送をモデル化する．
ブシネスク近似を利用する熱方程式と組み合せる粘性ナビエ・ストークス方程式を設定する．ベクトル化した方程式を以下に挙げる．
先ほども述べたように，成分はFluidFlowPDEComponentとHeatTransferPDEComponentの関数を使って生成することも可能である．
時間積分の進行と，細分化されたメッシュを使い，速度 
と 
および温度 
を二次で，圧力 
を一次で補間しながら，偏微分方程式を解くのにかかる総時間を管理する．
興味があれば，切り取る部分を変更して作った別の速度場を調べてみるとよい．
流量，ブシネスク(Boussinesq)近似，および適用可能な境界条件についての詳細は，層流のモノグラフと流量モデルのガイドページに記載されている．