WOLFRAM

Wolfram 语言与系统 参考资料中心
Wolfram 语言首页 »

AlternatingFactorial
✖
AlternatingFactorial

✖

给出交替阶乘 TemplateBox[{n}, AlternatingFactorial].

更多信息

范例

打开所有单元关闭所有单元

基本范例  (6)常见实例总结

计算前几个交替阶乘数：

In[1]:=1
✖
https://wolfram.com/xid/0mlcfc7ep4si-cfi83b
Out[1]=1

在实数的子集上以对数刻度绘制值:

In[1]:=1
✖
https://wolfram.com/xid/0mlcfc7ep4si-4uocp
Out[1]=1

在复数的子集上绘图：

In[1]:=1
✖
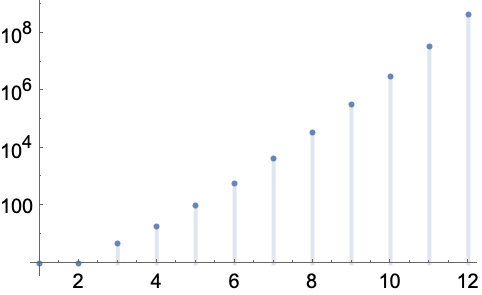
https://wolfram.com/xid/0mlcfc7ep4si-b7f34n
Out[1]=1

以其他函数的形式展开交替阶乘：

In[1]:=1
✖
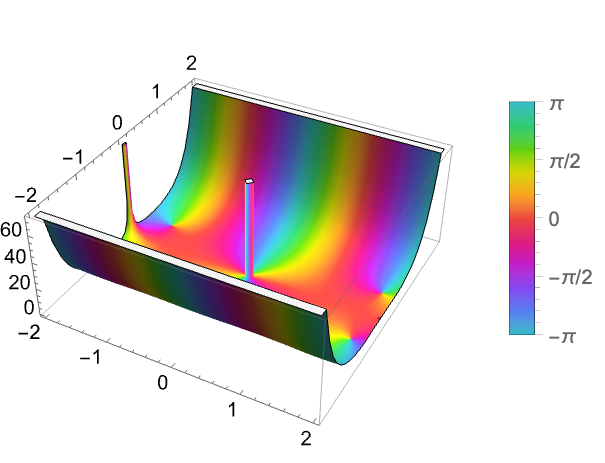
https://wolfram.com/xid/0mlcfc7ep4si-v46voh
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0mlcfc7ep4si-jqvg93
Out[2]=2

给出以下交替和的解析形式：

In[1]:=1
✖
https://wolfram.com/xid/0mlcfc7ep4si-hmlp64
Out[1]=1

交替阶乘数给出以下递归式的解：

In[1]:=1
✖
https://wolfram.com/xid/0mlcfc7ep4si-p7ljho
In[2]:=2
✖
https://wolfram.com/xid/0mlcfc7ep4si-384vzm
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0mlcfc7ep4si-jlrdhp
Out[3]=3

范围  (18)标准用法实例范围调查

数值计算  (6)

数值化计算：

In[1]:=1
✖
https://wolfram.com/xid/0mlcfc7ep4si-itrtf
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0mlcfc7ep4si-cksbl4
Out[2]=2

高精度计算：

In[1]:=1
✖
https://wolfram.com/xid/0mlcfc7ep4si-b0wt9
Out[1]=1

输出的精度与输入的精度一致：

In[2]:=2
✖
https://wolfram.com/xid/0mlcfc7ep4si-xth5g
Out[2]=2

AlternatingFactorial 可以接受复数输入：

In[1]:=1
✖
https://wolfram.com/xid/0mlcfc7ep4si-hfml09
Out[1]=1

高精度的高效计算：

In[1]:=1
✖
https://wolfram.com/xid/0mlcfc7ep4si-di5gcr
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0mlcfc7ep4si-bq2c6r
Out[2]=2

自动逐项计算数组中每个元素的值：

In[1]:=1
✖
https://wolfram.com/xid/0mlcfc7ep4si-fk4yi
Out[1]=1

或用 MatrixFunction 计算矩阵形式的 AlternatingFactorial 函数：

In[2]:=2
✖
https://wolfram.com/xid/0mlcfc7ep4si-fflfq4
Out[2]=2

用 Interval 和 CenteredInterval 对象计算最坏情况下的区间：

In[1]:=1
✖
https://wolfram.com/xid/0mlcfc7ep4si-dj6d9x
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0mlcfc7ep4si-f892wm
Out[2]=2

或用 Around 计算一般情况下的统计区间：

In[3]:=3
✖
https://wolfram.com/xid/0mlcfc7ep4si-cw18bq
Out[3]=3

特殊值  (3)

在固定点的 AlternatingFactorial 的值：

In[1]:=1
✖
https://wolfram.com/xid/0mlcfc7ep4si-nww7l
Out[1]=1

零处的值：

In[1]:=1
✖
https://wolfram.com/xid/0mlcfc7ep4si-e41pf2
Out[1]=1

符号式计算：

In[1]:=1
✖
https://wolfram.com/xid/0mlcfc7ep4si-eswwm
Out[1]=1

可视化  (2)

绘制 AlternatingFactorial 的绝对值:

In[1]:=1
✖
https://wolfram.com/xid/0mlcfc7ep4si-ecj8m7
Out[1]=1

绘制 TemplateBox[{z}, AlternatingFactorial] 实部：

In[1]:=1
✖
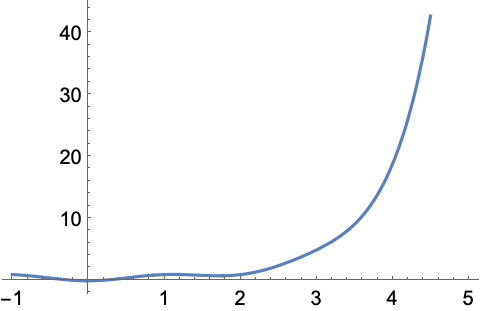
https://wolfram.com/xid/0mlcfc7ep4si-kgd8nu
Out[1]=1

绘制 TemplateBox[{z}, AlternatingFactorial] 虚部：

In[2]:=2
✖
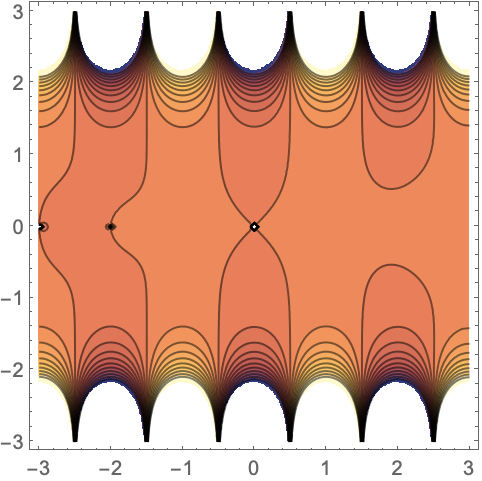
https://wolfram.com/xid/0mlcfc7ep4si-f3fwli
Out[2]=2

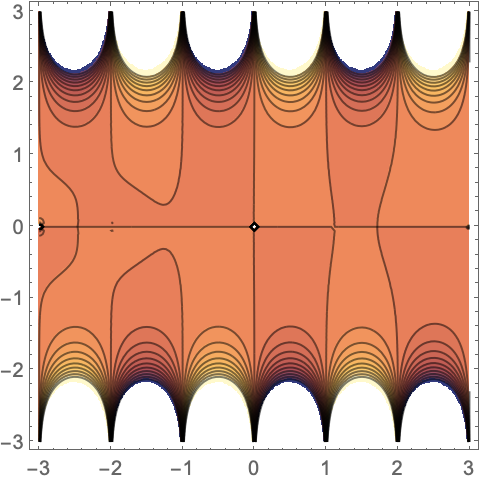
函数属性  (7)

AlternatingFactorial 的实域：

In[1]:=1
✖
https://wolfram.com/xid/0mlcfc7ep4si-cl7ele
Out[1]=1

复数域：

In[2]:=2
✖
https://wolfram.com/xid/0mlcfc7ep4si-de3irc
Out[2]=2

TraditionalForm 格式化：

In[1]:=1
✖
https://wolfram.com/xid/0mlcfc7ep4si-efpvd0

AlternatingFactorial 不是解析函数：

In[1]:=1
✖
https://wolfram.com/xid/0mlcfc7ep4si-gva6yl
Out[1]=1

AlternatingFactorial 在 z≤-2 有奇点和断点：

In[2]:=2
✖
https://wolfram.com/xid/0mlcfc7ep4si-fyfbxx
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0mlcfc7ep4si-5vh4e
Out[3]=3

AlternatingFactorial 既不是非递减也不是非递增：

In[1]:=1
✖
https://wolfram.com/xid/0mlcfc7ep4si-2ra8g
Out[1]=1

AlternatingFactorial 不是单射函数：

In[1]:=1
✖
https://wolfram.com/xid/0mlcfc7ep4si-c9npzh
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0mlcfc7ep4si-b5buvp
Out[2]=2

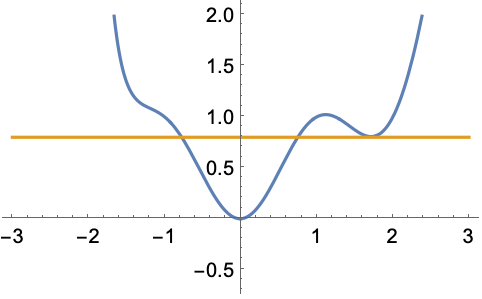
AlternatingFactorial 不是非负也不是非正：

In[1]:=1
✖
https://wolfram.com/xid/0mlcfc7ep4si-dvzykj
Out[1]=1

该函数在非负实数上为非负函数：

In[2]:=2
✖
https://wolfram.com/xid/0mlcfc7ep4si-estge4
Out[2]=2

AlternatingFactorial 不是凸函数也不是凹函数：

In[1]:=1
✖
https://wolfram.com/xid/0mlcfc7ep4si-l0srvu
Out[1]=1

应用  (1)用该函数可以解决的问题范例

AlternatingFactorial 可以在正整数上定义如下：

In[1]:=1
✖
https://wolfram.com/xid/0mlcfc7ep4si-i19x6t
Out[1]=1

对特定数值验证公式：

In[2]:=2
✖
https://wolfram.com/xid/0mlcfc7ep4si-d1q8s3
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0mlcfc7ep4si-ot04rg
Out[3]=3
Wolfram Research (2014)，AlternatingFactorial，Wolfram 语言函数，https://reference.wolfram.com/language/ref/AlternatingFactorial.html.
✖
Wolfram Research (2014)，AlternatingFactorial，Wolfram 语言函数，https://reference.wolfram.com/language/ref/AlternatingFactorial.html.

文本

Wolfram Research (2014)，AlternatingFactorial，Wolfram 语言函数，https://reference.wolfram.com/language/ref/AlternatingFactorial.html.

✖
Wolfram Research (2014)，AlternatingFactorial，Wolfram 语言函数，https://reference.wolfram.com/language/ref/AlternatingFactorial.html.

CMS

Wolfram 语言. 2014. "AlternatingFactorial." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/AlternatingFactorial.html.

✖
Wolfram 语言. 2014. "AlternatingFactorial." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/AlternatingFactorial.html.

APA

Wolfram 语言. (2014). AlternatingFactorial. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/AlternatingFactorial.html 年

✖
Wolfram 语言. (2014). AlternatingFactorial. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/AlternatingFactorial.html 年

BibTeX

@misc{reference.wolfram_2025_alternatingfactorial, author="Wolfram Research", title="{AlternatingFactorial}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/AlternatingFactorial.html}", note=[Accessed: 02-April-2025 ]}

✖
@misc{reference.wolfram_2025_alternatingfactorial, author="Wolfram Research", title="{AlternatingFactorial}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/AlternatingFactorial.html}", note=[Accessed: 02-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_alternatingfactorial, organization={Wolfram Research}, title={AlternatingFactorial}, year={2014}, url={https://reference.wolfram.com/language/ref/AlternatingFactorial.html}, note=[Accessed: 02-April-2025 ]}

✖
@online{reference.wolfram_2025_alternatingfactorial, organization={Wolfram Research}, title={AlternatingFactorial}, year={2014}, url={https://reference.wolfram.com/language/ref/AlternatingFactorial.html}, note=[Accessed: 02-April-2025 ]}