BetaNegativeBinomialDistribution

BetaNegativeBinomialDistribution[α,β,n]

ベータ分布の母数 α および β で試行が n 回成功した，ベータの負の二項混合分布を表す．

詳細

予備知識

  • BetaNegativeBinomialDistribution[α,β,n]は，整数値 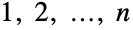において定義される離散統計分布を表す．母数 α および β は形状母数として知られる正の実数で，確率密度関数(PDF)の全体的な形と動作を決定する．ベータの負の二項分布は離散PDFを持つ．このPDFは，α および β の値によって，単調増加または単調減少の値を持つか，単峰性になるかする．ベータの負の二項分布は，逆Markov–Pólya分布，ベータパスカル分布，一般化されたウェアリング分布として参照されることもある．
  • ベータの負の二項分布は，既知回数のベルヌーイ試行の成功確率 p がランダムであり，同伴二項分布がベータ分布(BetaDistribution)に従う成功確率 p を持ち，失敗の分布が研究された，ベルヌーイ分布(BernoulliDistribution)および負の二項分布(NegativeBinomialDistribution)を抽象化したものと考えることができる．ベイズの的解釈では，これは，ベータの負の二項分布が，成功確率 p についての事前分布がベータ分布に従う負の二項変数の事後予測分布として現れたことを意味する．
  • ベータの負の二項分布が文書の中で最初に言及されたのは，1950年代のKemp等の業績中である．これは，ベータ二項分布(BetaBinomialDistribution)を導出し研究する際に著者たちが使ったメソッドと類似のメソッドによって得られた．ベータの負の二項分布を使って数多くの現実世界の現象をモデル化することができる．例えば，ベータの負の二項分布を使って，特別な取出し規則と追加的な交換があるポリヤの壷モデルを逆サンプリングすることができる．より最近では，ベータの負の二項分布は伝染病の分布のモデル化に応用されており，さまざまなリスクに晒された事故多発地域における事故の分布を説明するために事故理論にも使用されている
  • RandomVariateを使ってベータの負の二項分布から，1つあるいは複数の機械精度あるいは任意精度（後者はWorkingPrecisionオプションを介す）の擬似乱数変量を得ることができる．Distributed[x,BetaNegativeBinomialDistribution[α,β,n]]（より簡略すると xBetaNegativeBinomialDistribution[α,β,n]）を使って，確率変数 x がベータの負の二項分布に従って分布していると宣言することができる．このような宣言は，Probability，NProbability，Expectation，NExpectation等の関数で使うことができる．
  • 確率密度関数および累積分布関数は，PDF[BetaNegativeBinomialDistribution[α,β,n],x]およびCDF[BetaNegativeBinomialDistribution[α,β,n],x]を使って得られることがある．平均，中央値，分散，原点の周りのモーメント，中心モーメントは，それぞれMean，Median，Variance，Moment，CentralMomentを使って計算することができる．これらの数量はDiscretePlotを使って可視化することができる．
  • DistributionFitTestを使って，与えられたデータ集合がベータの負の二項分布と一致するかどうかを検定することが，EstimatedDistributionを使って与えられたデータからベータの負の二項パラメトリック分布を推定することが，FindDistributionParametersを使ってデータをベータの負の二項分布にフィットすることができる．ProbabilityPlotを使って記号的なベータの負の二項分布のCDFに対する与えられたデータのCDFのプロットを生成することが，QuantilePlotを使って記号的なベータの負の二項分布の変位値に対する与えられたデータの変位値のプロットを生成することができる．
  • TransformedDistributionを使って変換されベータの負の二項分布を表すことが，CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが，TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる．CopulaDistributionを使ってベータの負の二項分布を含む高次元分布を構築することが，ProductDistributionを使ってベータの負の二項分布を含む独立成分分布の結合分布を計算することができる．
  • BetaNegativeBinomialDistributionは他の数多くの統計分布と関係がある．先に記したように，BetaNegativeBinomialDistributionはNegativeBinomialDistributionとBetaDistributionの両方の特徴を組み合せている．この事実は，ParameterMixtureDistribution[NegativeBinomialDistribution[n,p],pBetaDistribution[α,β]]を評価すると BetaNegativeBinomialDistribution[α,β,n]になる事実によって確かなものとなる．同様に，WaringYuleDistributionは，WaringYuleDistribution[α,β]がBetaNegativeBinomialDistribution[α,β,1]と同じPDFを持つという意味で，BetaNegativeBinomialDistributionの特殊ケースである．BetaNegativeBinomialDistributionは，非常に自然な方法でBetaBinomialDistributionと関連しており，NegativeMultinomialDistributionとDirichletDistributionが，NegativeBinomialDistributionとBetaDistributionそれぞれの高次元の類似物であるという事実によって，BetaNegativeBinomialDistributionはいわゆるディリクレの負の多次元分布の1次元における類似物であると考えることができる．

例題

すべて開くすべて閉じる

例  (3)

確率質量関数：

累積分布関数：

平均と分散：

スコープ  (7)

ベータの負の二項分布から擬似乱数のサンプルを生成する：

このヒストグラムを確率密度関数と比較する：

分布母数推定：

サンプルデータから分布母数を推定する：

サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する：

歪度：

尖度：

母数の関数としての閉形式の種々のモーメント：

Moment：

CentralMoment：

FactorialMoment：

記号次数の閉形式：

Cumulant：

ハザード関数：

分位関数：

アプリケーション  (2)

BetaNegativeBinomialDistributionのCDFは右連続関数の例である：

におけるベータ分布を仮定して，10回成功するまでに少なくとも50回失敗する確率：

固定された の値について確率を計算し，これを平均して確かめる：

特性と関係  (5)

負の整数，n より大きい整数，あるいは整数ではない数を得る確率は0である：

他の分布との関係：

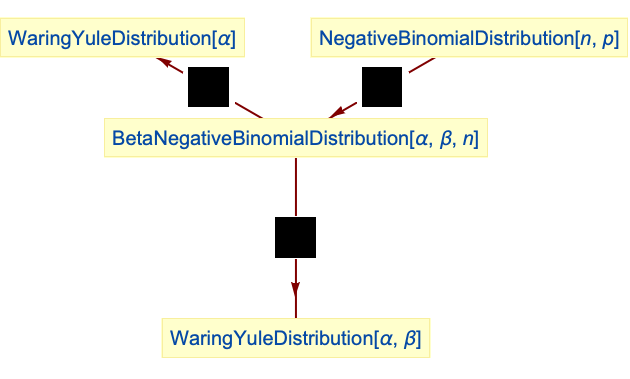
WaringYuleDistributionは負のベータ二項分布の特殊ケースである：

WaringYuleDistributionはベータの負の二項分布の特殊ケースである：

ベータの負の二項分布はNegativeBinomialDistributionとBetaDistributionの混合である：

考えられる問題  (2)

BetaNegativeBinomialDistributionは，α，β，n のいずれかが正ではない場合は定義されない：

記号出力に無効な母数値を代入すると意味のない結果となる：

Wolfram Research (2007), BetaNegativeBinomialDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/BetaNegativeBinomialDistribution.html.

テキスト

Wolfram Research (2007), BetaNegativeBinomialDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/BetaNegativeBinomialDistribution.html.

CMS

Wolfram Language. 2007. "BetaNegativeBinomialDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/BetaNegativeBinomialDistribution.html.

APA

Wolfram Language. (2007). BetaNegativeBinomialDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BetaNegativeBinomialDistribution.html

BibTeX

@misc{reference.wolfram_2024_betanegativebinomialdistribution, author="Wolfram Research", title="{BetaNegativeBinomialDistribution}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/BetaNegativeBinomialDistribution.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_betanegativebinomialdistribution, organization={Wolfram Research}, title={BetaNegativeBinomialDistribution}, year={2007}, url={https://reference.wolfram.com/language/ref/BetaNegativeBinomialDistribution.html}, note=[Accessed: 22-November-2024 ]}