BinomialPointProcess
✖
BinomialPointProcess
詳細

- BinomialPointProcess[n,reg]は reg に一様に分布した総数 n 個の点を生成する.
- 一般的な用途は,領域内の既知のワイヤレストランシーバの数や水槽内の魚の数のように点の総数が指定されている場合である.
- BinomialPointProcessとPoissonPointProcessは,どちらも領域上の点の一様分布を返す.前者は点の数が決定論的で,後者は点の数がランダムである.
- 有界の部分領域
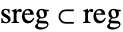 内の点の数はBinomialDistribution[n,p]に従い,p=RegionMeasure[sreg]/RegionMeasure[reg]である.
内の点の数はBinomialDistribution[n,p]に従い,p=RegionMeasure[sreg]/RegionMeasure[reg]である. - 二項点過程についての reg の互いに素な部分領域内の点の数は独立ではない.
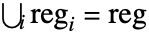 を満足する互いに素な部分領域
を満足する互いに素な部分領域 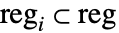 について,体積
について,体積 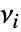 の部分領域
の部分領域 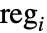 内の点の数の接合分布はMultinomialDistribution[n,{ν1/ν,…,νn/ν}]に従う.ただし,
内の点の数の接合分布はMultinomialDistribution[n,{ν1/ν,…,νn/ν}]に従う.ただし,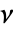 は reg の体積である.
は reg の体積である.- BinomialPointProcess[n,reg]は事象
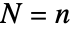 を条件とするPoissonPointProcess[μ]である.ただし,
を条件とするPoissonPointProcess[μ]である.ただし, はPointCountDistribution[PoissonPointProcess[μ],reg]に従う確率変数である.
はPointCountDistribution[PoissonPointProcess[μ],reg]に従う確率変数である. - BinomialPointProcessでは,n は任意の正の整数でよく,reg は任意のパラメータフリーの領域でよい.
- BinomialPointProcessは,RipleyKやRandomPointConfiguration等の関数と一緒に使うことができる.
例題
すべて開くすべて閉じる例 (2)基本的な使用例
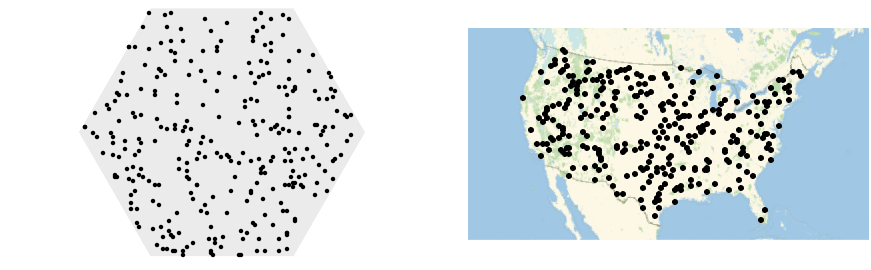
BinomialPointProcessからサンプルを取る:
https://wolfram.com/xid/0e5c7rkfrwmlyq-l37xwd

https://wolfram.com/xid/0e5c7rkfrwmlyq-6q6pq
https://wolfram.com/xid/0e5c7rkfrwmlyq-gwc84f

https://wolfram.com/xid/0e5c7rkfrwmlyq-hdfqz
https://wolfram.com/xid/0e5c7rkfrwmlyq-hc6ki4
https://wolfram.com/xid/0e5c7rkfrwmlyq-bi5nn
スコープ (2)標準的な使用例のスコープの概要
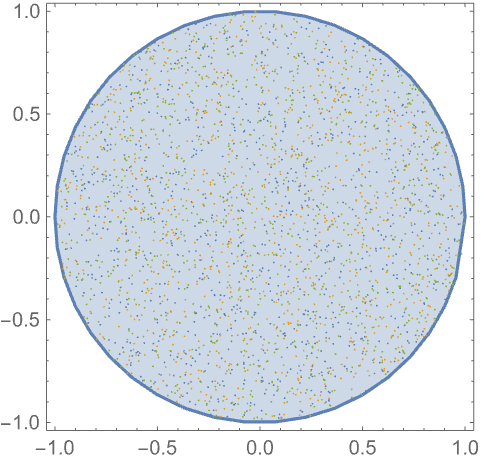
RegionEmbeddingDimensionがRegionDimensionと等しい任意の有効なRegionQからサンプルを取る:
https://wolfram.com/xid/0e5c7rkfrwmlyq-qxrhco
https://wolfram.com/xid/0e5c7rkfrwmlyq-dafvpv
https://wolfram.com/xid/0e5c7rkfrwmlyq-ydq337

https://wolfram.com/xid/0e5c7rkfrwmlyq-h8cla8
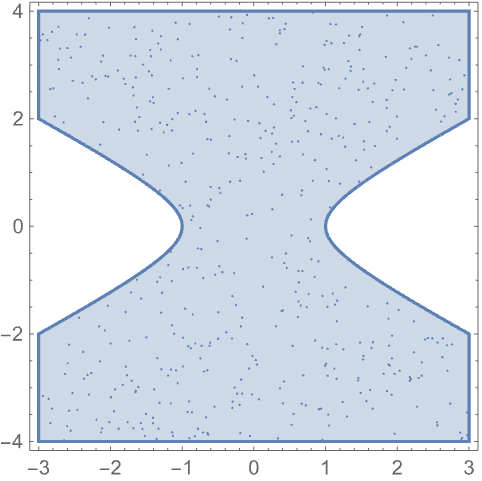
https://wolfram.com/xid/0e5c7rkfrwmlyq-1usyu9
https://wolfram.com/xid/0e5c7rkfrwmlyq-zb4or3
https://wolfram.com/xid/0e5c7rkfrwmlyq-kv5v29

https://wolfram.com/xid/0e5c7rkfrwmlyq-we3oyo
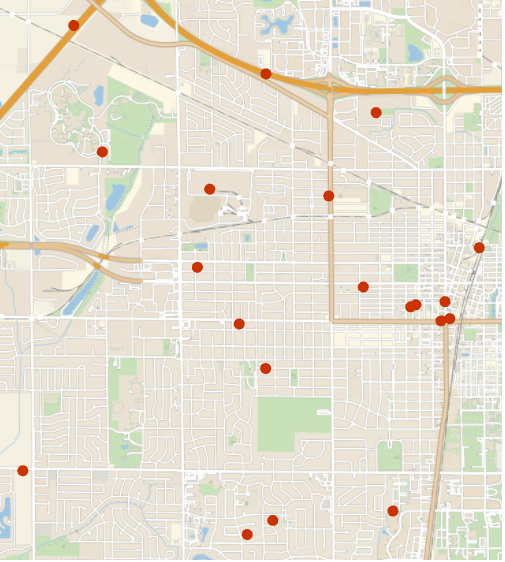
アプリケーション (1)この関数で解くことのできる問題の例
特性と関係 (4)この関数の特性および他の関数との関係
BinomialPointProcess内の点の数は n によって定義される:
https://wolfram.com/xid/0e5c7rkfrwmlyq-hcejl3
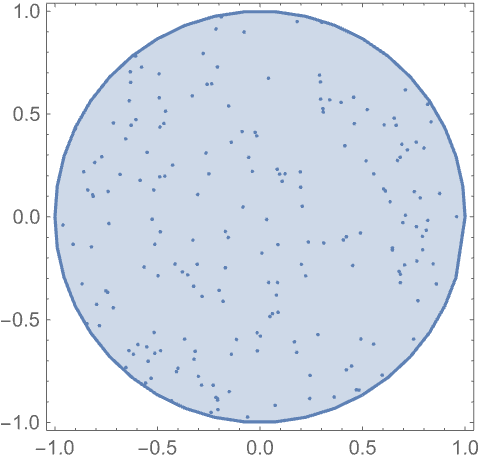
単位円板上でBinomialPointProcessのシミュレーションを行う:
https://wolfram.com/xid/0e5c7rkfrwmlyq-7vkzhn
https://wolfram.com/xid/0e5c7rkfrwmlyq-jjyqjn

有界部分集合上の対応するPointCountDistribution:
https://wolfram.com/xid/0e5c7rkfrwmlyq-5gmn7
https://wolfram.com/xid/0e5c7rkfrwmlyq-d5w2t3

https://wolfram.com/xid/0e5c7rkfrwmlyq-c7nyut
https://wolfram.com/xid/0e5c7rkfrwmlyq-2k7h5r
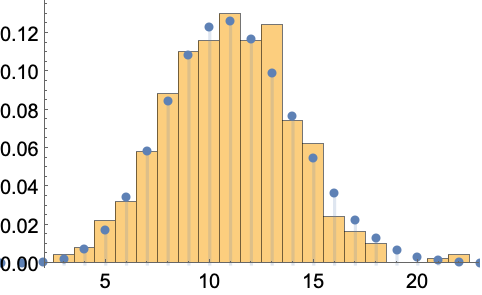
BinomialDistributionを点の数にフィットする:
https://wolfram.com/xid/0e5c7rkfrwmlyq-gr4k9c
https://wolfram.com/xid/0e5c7rkfrwmlyq-m46usn
https://wolfram.com/xid/0e5c7rkfrwmlyq-bk6ev7
領域被覆上のPointCountDistribution:
https://wolfram.com/xid/0e5c7rkfrwmlyq-uspmrn
https://wolfram.com/xid/0e5c7rkfrwmlyq-zdyvdj
https://wolfram.com/xid/0e5c7rkfrwmlyq-0hh6u9
https://wolfram.com/xid/0e5c7rkfrwmlyq-kop1b4

https://wolfram.com/xid/0e5c7rkfrwmlyq-i49zp
https://wolfram.com/xid/0e5c7rkfrwmlyq-2j6bhn
https://wolfram.com/xid/0e5c7rkfrwmlyq-dcc7zf
https://wolfram.com/xid/0e5c7rkfrwmlyq-60ixxo
https://wolfram.com/xid/0e5c7rkfrwmlyq-xs30cs
https://wolfram.com/xid/0e5c7rkfrwmlyq-fwyxlc
https://wolfram.com/xid/0e5c7rkfrwmlyq-fugl3p
https://wolfram.com/xid/0e5c7rkfrwmlyq-em07kv
https://wolfram.com/xid/0e5c7rkfrwmlyq-p79axg
https://wolfram.com/xid/0e5c7rkfrwmlyq-1nahei
https://wolfram.com/xid/0e5c7rkfrwmlyq-kr3wtf
https://wolfram.com/xid/0e5c7rkfrwmlyq-bdl658
Wolfram Research (2020), BinomialPointProcess, Wolfram言語関数, https://reference.wolfram.com/language/ref/BinomialPointProcess.html.テキスト
Wolfram Research (2020), BinomialPointProcess, Wolfram言語関数, https://reference.wolfram.com/language/ref/BinomialPointProcess.html.
Wolfram Research (2020), BinomialPointProcess, Wolfram言語関数, https://reference.wolfram.com/language/ref/BinomialPointProcess.html.CMS
Wolfram Language. 2020. "BinomialPointProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/BinomialPointProcess.html.
Wolfram Language. 2020. "BinomialPointProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/BinomialPointProcess.html.APA
Wolfram Language. (2020). BinomialPointProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BinomialPointProcess.html
Wolfram Language. (2020). BinomialPointProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BinomialPointProcess.htmlBibTeX
@misc{reference.wolfram_2025_binomialpointprocess, author="Wolfram Research", title="{BinomialPointProcess}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/BinomialPointProcess.html}", note=[Accessed: 12-May-2025
]}BibLaTeX
@online{reference.wolfram_2025_binomialpointprocess, organization={Wolfram Research}, title={BinomialPointProcess}, year={2020}, url={https://reference.wolfram.com/language/ref/BinomialPointProcess.html}, note=[Accessed: 12-May-2025
]}