BinomialPointProcess[n,reg]
代表一个在区域 reg 中有 n 个点的二项式点过程.


BinomialPointProcess
BinomialPointProcess[n,reg]
代表一个在区域 reg 中有 n 个点的二项式点过程.
更多信息

- BinomialPointProcess[n,reg] 生成数量等于 n 的在区域 reg 内均匀分布的点.
- 一般使用情形包括当点的总数已被指定的情形,如已知一个区域内无线接收器的数量、水族馆内鱼的数量等.
- BinomialPointProcess 和 PoissonPointProcess 都会在一个区域上生成均匀分布的点. 前者使用一个确定的点的数量,而后者使用一个随机的点数量.
- 在一个有边界的子区域
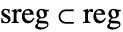 内,点数量遵从 BinomialDistribution[n,p],其中 p=RegionMeasure[sreg]/RegionMeasure[reg].
内,点数量遵从 BinomialDistribution[n,p],其中 p=RegionMeasure[sreg]/RegionMeasure[reg]. - 二项式点过程的 reg 的分离子区域中点的数量不是独立的.
- 对于满足
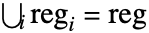 的分离子区域
的分离子区域 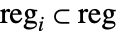 而言,在体积为
而言,在体积为 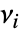 的子区域
的子区域 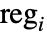 中点的数量的联合分布遵循 MultinomialDistribution[n,{ν1/ν,…,νn/ν}],其中
中点的数量的联合分布遵循 MultinomialDistribution[n,{ν1/ν,…,νn/ν}],其中 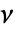 是区域 reg 的体积.
是区域 reg 的体积. - BinomialPointProcess[n,reg] 是以事件
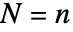 为条件的 PoissonPointProcess[μ],其中
为条件的 PoissonPointProcess[μ],其中 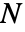 是一个随机变量,遵循 PointCountDistribution[PoissonPointProcess[μ],reg].
是一个随机变量,遵循 PointCountDistribution[PoissonPointProcess[μ],reg]. - BinomialPointProcess 允许 n 是任何正整数,且 reg 可以是任何无参数区域.
- BinomialPointProcess 可与诸如 RipleyK 和 RandomPointConfiguration 这样的函数一起使用.
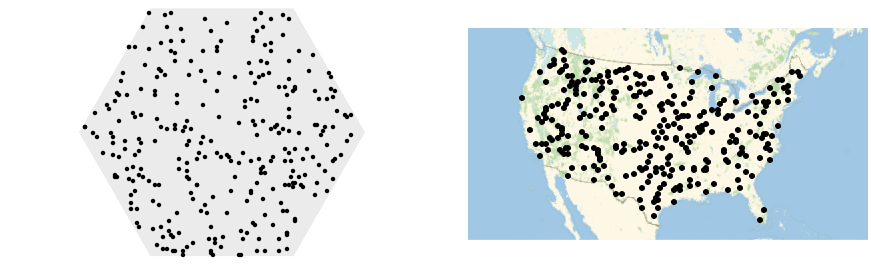
范例
打开所有单元 关闭所有单元基本范例 (2)
范围 (2)
属性和关系 (4)
BinomialPointProcess 中的点的数量由 n 定义:
在单位圆盘上模拟 BinomialPointProcess:
有边界的子集上对应的 PointCountDistribution:
将 BinomialDistribution 拟合到点数:
区域覆盖上的 PointCountDistribution:
文本
Wolfram Research (2020),BinomialPointProcess,Wolfram 语言函数,https://reference.wolfram.com/language/ref/BinomialPointProcess.html.
CMS
Wolfram 语言. 2020. "BinomialPointProcess." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/BinomialPointProcess.html.
APA
Wolfram 语言. (2020). BinomialPointProcess. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/BinomialPointProcess.html 年
BibTeX
@misc{reference.wolfram_2025_binomialpointprocess, author="Wolfram Research", title="{BinomialPointProcess}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/BinomialPointProcess.html}", note=[Accessed: 13-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_binomialpointprocess, organization={Wolfram Research}, title={BinomialPointProcess}, year={2020}, url={https://reference.wolfram.com/language/ref/BinomialPointProcess.html}, note=[Accessed: 13-February-2026]}