領域 reg をBoundaryMeshRegionに離散化する.
BoundaryDiscretizeRegion[reg,{{xmin,xmax},…}]
境界![]() に制限する.
に制限する.




BoundaryDiscretizeRegion
領域 reg をBoundaryMeshRegionに離散化する.
BoundaryDiscretizeRegion[reg,{{xmin,xmax},…}]
境界![]() に制限する.
に制限する.
詳細とオプション

- BoundaryDiscretizeRegionは,境界評価としても知られている.
- BoundaryDiscretizeRegionは,事実上,領域 reg の完全な次元部分の境界を離散化する.
- 領域 reg は,ConstantRegionQでRegionEmbeddingDimensionが3以下のものなら何でもよい.
- BoundaryDiscretizeRegionには,BoundaryMeshRegionと同じオプションに次の追加・変更を加えたものが使える.
-
AccuracyGoal Automatic 求める確度の桁数 MaxCellMeasure Automatic 最大セル測度 Method Automatic 使用するメソッド PerformanceGoal $PerformanceGoal 速度と質のどちらを考慮するか PrecisionGoal Automatic 目標とする精度の桁数 - AccuracyGoal->a およびPrecisionGoal->p とすると,領域 reg あるいは離散化された領域 dreg とRegionSymmetricDifference[reg,dreg]内の任意の点の間の最大距離を
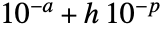 未満に保とうと試みられる.ただし,
未満に保とうと試みられる.ただし,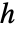 は境界ボックスの対角線の長さである.
は境界ボックスの対角線の長さである. - m>0であるMaxCellMeasure->m のとき,境界次元 d-1(d は領域次元)中のセル測度は m に制限される.特定の次元についての測度の極限はMaxCellMeasure->{…,di->mi,…}で指定することができる.

例題
すべて開く すべて閉じるスコープ (24)
1D領域 (5)
LineおよびIntervalは,1Dにおける全次元の領域である:
ImplicitRegionは,変数が1つの場合は1Dである:
ParametricRegionは,1つの関数しか持たない場合は,1Dである:
1DにおけるBooleanRegion:
DiscretizeRegionを使って低次元成分も離散化する:
2D領域 (8)
Rectangle,Disk,Simplexは,2Dで全次元になり得る特殊領域である:
Disk:
ImplicitRegionは,変数が2つあれば,2Dである:
有界ではない領域については,指定された領域についての離散化を切り取る:
ParametricRegionは,関数が2つであれば,2Dである:
厳密な領域が2つ与えられると,ParametricRegionを使ってそのMinkowski和を表すことができる:
2DにおけるRegionUnion:
GeoGridPositionを使った多角形:
3D領域 (5)
Cuboid,Ellipsoid,Simplexは,3Dで全次元であり得る特殊領域である:
ImplicitRegionは,変数が厳密に3個であれば3Dである:
ParametricRegionは,厳密に3つの関数を持つときは3Dにある:

詳細 (2)
離散化におけるセルの測度はMaxCellMeasureを使って制御できる:
デフォルトで,数として与えられた場合は境界次元に適用される:
面積が a のとき,長さ l は,辺の長さが l の三角形の面積が a になるように計算される:
同じ指定でTriangulateMeshを使うと辺の近くの品質が保たれる:
非線形領域については,境界セルの測度はいくつかのオプションに依存する:
任意の線分の長さはMaxCellMeasureで制御できることがある:
デフォルトのPrecisionGoalには,曲線が視覚的に滑らかになるような値が選ば得る:
MaxCellMeasure->∞を使って境界測度を精度に基づかせることができる:
PrecisionGoal->Noneを使って境界測度をMaxCellMeasureに基づかせることができる:
AccuracyGoal->a を使って絶対許容度![]() を指定することができる:
を指定することができる:
MaxCellMeasureは,デフォルトでは境界次元に適用される:
品質 (4)
離散化におけるセルの測度はMaxCellMeasureで制御することができる:
AccuracyGoalを使い,離散化境界が厳密な境界に近いものであるようにする:
より高いAccuracyGoalによる離散化は,真の境界により近い:
PrecisionGoalを使い,離散化された境界が厳密な境界に近いものであるようにする:
より高いPrecisionGoalによる離散化は,真の境界により近い:
高品質の離散化のために,PerformanceGoalを"Quality"に設定する:
オプション (24)
MaxCellMeasure (2)
MaxCellMeasure->m のとき,境界セルの大きさは ![]() 以下である:
以下である:
3Dでは,表面積はMaxCellMeasureで制御される:
MeshCellHighlight (3)
MeshCellHighlightを使ってBoundaryMeshRegionの一部のハイライトを指定することができる:
面を透明にすることで3DのBoundaryMeshRegionの内部構造を見ることができる:
MeshCellLabel (3)
MeshCellLabelを使ってBoundaryMeshRegionの一部にラベルを付けることができる:
MeshCellMarker (1)
MeshCellMarkerを使ってBoundaryMeshRegionの一部に値を割り当てることができる:
MeshCellLabelを使ってマーカーを示す:
MeshCellShapeFunction (2)
MeshCellShapeFunctionを使ってBoundaryMeshRegionの一部についての関数を指定することができる:
MeshCellStyle (3)
MeshCellStyleを使ってBoundaryMeshRegionの一部のスタイルを指定することができる:
面を透過的にすることで,3DのBoundaryMeshRegionの内部構造を見ることができる:
Method (6)
"Continuation"法は,多くの場合,コーナー,尖端,際立った変化をきわめてうまく結合する曲線連続法を使う:
"RegionPlot"メソッドは,RegionPlotからの出力を向上させることに基づき,より速いこともある:
"DiscretizeGraphics"メソッドは,グラフィックスプリミティブに最適化されている:
3D領域についての"RegionPlot3D"メソッドは,RegionPlot3Dに基づいている:
3D領域についての"ContourPlot3D"メソッドは,ContourPlot3Dに基づいている:
アプリケーション (2)
特性と関係 (5)
BoundaryDiscretizeRegionの出力はBoundaryMeshRegionである:
境界離散化を与えられると,TriangulateMeshは内部を離散化することができる:
低次元成分は失われるが,DiscretizeRegionで表すことができる:
BoundaryDiscretizeRegionは,穴がある領域を離散化することができる:
BoundaryDiscretizeRegionは,不連続な成分がある領域を離散化することができる:
関連するガイド
-
▪
- メッシュベースの幾何学的領域 ▪
- 幾何学的計算
テキスト
Wolfram Research (2014), BoundaryDiscretizeRegion, Wolfram言語関数, https://reference.wolfram.com/language/ref/BoundaryDiscretizeRegion.html (2015年に更新).
CMS
Wolfram Language. 2014. "BoundaryDiscretizeRegion." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/BoundaryDiscretizeRegion.html.
APA
Wolfram Language. (2014). BoundaryDiscretizeRegion. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BoundaryDiscretizeRegion.html
BibTeX
@misc{reference.wolfram_2025_boundarydiscretizeregion, author="Wolfram Research", title="{BoundaryDiscretizeRegion}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/BoundaryDiscretizeRegion.html}", note=[Accessed: 06-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_boundarydiscretizeregion, organization={Wolfram Research}, title={BoundaryDiscretizeRegion}, year={2015}, url={https://reference.wolfram.com/language/ref/BoundaryDiscretizeRegion.html}, note=[Accessed: 06-February-2026]}