RegionSymmetricDifference[reg1,reg2,…]
represents the symmetric difference of the regions reg1, reg2, ….


RegionSymmetricDifference
RegionSymmetricDifference[reg1,reg2,…]
represents the symmetric difference of the regions reg1, reg2, ….
Details and Options

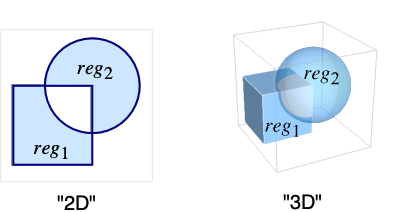
- A point p belongs to RegionSymmetricDifference[reg1,reg2,…] if it belongs to an odd number of regi.
- For BoundaryMeshRegion reg1 and reg2, RegionSymmetricDifference gives the smallest BoundaryMeshRegion that contains the difference of reg1 and reg2.
- For MeshRegion reg1 and reg2, RegionSymmetricDifference gives the smallest MeshRegion that contains the difference of reg1 and reg2.
- RegionSymmetricDifference takes the same options as Region.
Examples
open all close allBasic Examples (2)
Scope (10)
Special Regions (4)
A symmetric difference of Line regions:
A symmetric difference of Polygon regions:
A symmetric difference of two Cuboid regions:
A symmetric difference of regions with different RegionDimension:
Formula Regions (2)
A symmetric difference of ImplicitRegion objects is an ImplicitRegion:
A symmetric difference of ParametricRegion objects:
Mesh Regions (2)
A symmetric difference of BoundaryMeshRegion objects is a BoundaryMeshRegion:
A symmetric difference of full-dimensional MeshRegion objects is a MeshRegion:
Derived Regions (2)
A symmetric difference of BooleanRegion objects:
A symmetric difference of TransformedRegion objects:
Properties & Relations (5)
A point p belongs to RegionSymmetricDifference[reg1,reg2] if it belongs to an odd number of regi:
Use RegionMember to test membership:
RegionSymmetricDifference is a Boolean combination Xor of regions:
RegionSymmetricDifference can be found using RegionUnion and RegionDifference:
The RegionDimension of a symmetric difference is at most the max of the input dimensions:
This symmetric difference is two lines, and thus has dimension 1:
The RegionMeasure of a symmetric difference obeys a simple formula:
Simply subtract twice the measure of the intersection from the sum of the input measures:
Possible Issues (1)
Symmetric difference is defined only for regions with the same RegionEmbeddingDimension:
Related Guides
Text
Wolfram Research (2014), RegionSymmetricDifference, Wolfram Language function, https://reference.wolfram.com/language/ref/RegionSymmetricDifference.html (updated 2017).
CMS
Wolfram Language. 2014. "RegionSymmetricDifference." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/RegionSymmetricDifference.html.
APA
Wolfram Language. (2014). RegionSymmetricDifference. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RegionSymmetricDifference.html
BibTeX
@misc{reference.wolfram_2025_regionsymmetricdifference, author="Wolfram Research", title="{RegionSymmetricDifference}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/RegionSymmetricDifference.html}", note=[Accessed: 25-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_regionsymmetricdifference, organization={Wolfram Research}, title={RegionSymmetricDifference}, year={2017}, url={https://reference.wolfram.com/language/ref/RegionSymmetricDifference.html}, note=[Accessed: 25-February-2026]}