BoundingRegion

BoundingRegion[{pt1,pt2,…}]

点 pt1, pt2, …についての，軸に平行な最小の境界ボックスを与える．

BoundingRegion[{pt1,pt2,…},form]

タイプ form の境界領域を与える．

BoundingRegion[reg,form]

領域 reg の境界領域を与える．

詳細とオプション

  • BoundingRegionは，囲い込み領域あるいは外接領域としても知られている．
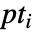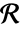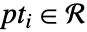  • 点集合 についての境界領域 は となる領域である．
  • 最適化された境界領域は，方向が定められた最小面積の長方形のように，境界領域についての特性が最小化されることが多い．計算には時間がかかることが多い．
  • 高速境界領域は，大抵の場合，多数の点に対して即座に境界領域を与えるが，方向が定められた最小面積の長方形のように最適化された境界領域ではないことがある．
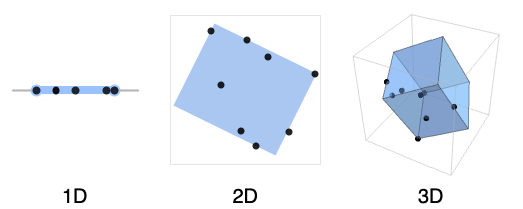
  • 1Dで指定可能な form
  • "MinInterval"最短区間
  • 2Dで指定可能な form
  • "MinRectangle"面積が最小の軸に平行な長方形
    "MinOrientedRectangle"面積が最小の方向が定められた長方形
    "MinConvexPolygon"面積が最小の凸多角形
    "MinDisk"面積が最小の円板
    "MinEllipse"面積が最小の楕円
    "FastOrientedRectangle"方向が定められた高速境界長方形
    "FastDisk"高速境界円板
    "FastEllipse"高速境界楕円
    "FastStadium"高速境界スタジアム
  • 3Dで指定可能な form
  • "MinCuboid"体積が最小の軸に平行な直方体
    "MinOrientedCuboid"体積が最小の方向が定められた直方体
    "MinConvexPolyhedron"体積が最小の凸多面体
    "MinBall"体積が最小の球体
    "MinEllipsoid"体積が最小の楕体
    "FastOrientedCuboid"方向が定められた高速直方体
    "FastBall"高速球体
    "FastEllipsoid"高速楕円体
    "FastCylinder"高速円柱
    "FastCapsule"高速カプセル
  • n Dで指定可能な form
  • "MinCuboid"最小測度の軸に平行な直方体
    "MinBall"最小測度の球体
    "MinEllipsoid"最小測度の楕円体
    "FastOrientedCuboid"方向が定められた高速直方体
    "FastBall"高速球体
    "FastEllipsoid"高速楕円体
  • BoundingRegion[reg]はBoundingRegion[reg,"MinCuboid"]に等しい，
  • 使用可能なオプション
  • PerformanceGoal$PerformanceGoal最適化するパフォーマンスの局面
    WorkingPrecision MachinePrecision計算精度

例題

すべて開くすべて閉じる

例  (4)

点集合を含む最小面積のDisk：

点集合を含む最小面積のRectangle：

任意に方向が定められた最小面積の長方形：

点集合を含む最小体積のBall：

点集合を含む最小体積のCuboid：

任意に方向が定められた最小体積の直方体：

スコープ  (28)

1D  (3)

"MinInterval"は1Dの点集合のためのものである：

大きい点集合に使うことができる：

メッシュ領域に使うことができる：

2D  (9)

"MinRectangle"は，軸と平行な最小面積のRectangleを与える：

大きい点集合に使うことができる：

"MinOrientedRectangle"は，軸と平行とは限らないが最小面積の長方形を与える：

大きい点集合に使うことができる：

"MinConvexPolygon"は点を含む最小面積の多角形を与える：

大きい点集合に使うことができる：

"MinDisk"は点を含む最小面積のDiskを与える：

大きい点集合に使うことができる：

"FastOrientedRectangle"は方向付けがされた境界長方形を与える．面積が可能な限り最小とは限らない：

大きい点集合に使うことができる：

"FastDisk"は境界Diskを与える．面積が可能な限り最小とは限らない：

大きい点集合に使うことができる：

"FastEllipse"は境界Ellipsoidを与える．面積が可能な限り最小とは限らない：

大きい点集合に使うことができる：

"FastStadium"は境界StadiumShapeを与える．面積が可能な限り最小とは限らない：

大きい点集合に使うことができる：

メッシュ領域の境界領域を求める：

3D  (11)

"MinCuboid"は最小体積の軸と平行なCuboidを与える：

大きい点集合に使うことができる：

"MinOrientedCuboid"は，軸と平行とは限らないが最小体積の直方体を与える：

大きい点集合に使うことができる：

"MinConvexPolyhedron"は，点を含む最小体積の多面体を与える：

大きい点集合に使うことができる：

"MinBall"は点を含む最小体積のBallを与える：

大きい点集合に使うことができる：

"FastOrientedCuboid"は方向付けがされた境界直方体を与える．体積が最小とは限らない：

大きい点集合に使うことができる：

"FastBall"は境界Ballを与える．その体積は可能な限り最小とは限らない：

大きい点集合に使うことができる：

"FastEllipsoid"は境界Ellipsoidを与える．体積が最小とは限らない：

大きい点集合に使うことができる：

"FastCylinder"は境界Cylinderを与える．体積が最小とは限らない：

大きい点集合に使うことができる：

"FastCapsule"は境界CapsuleShapeを与える．体積が最小とは限らない：

大きい点集合に使うことができる：

境界領域の体積を比較する：

メッシュ領域の境界領域を求める：

D  (5)

"MinCuboid"は軸と平行な測度値が最小のCuboidを与える：

大きい点集合に使うことができる：

より高次元に使うことができる：

"MinBall"は，点を含む測度値が最小のBallを与える：

大きい点集合に使うことができる：

より高次元に使うことができる：

厳密係数に使うことができる：

"FastOrientedCuboid"は，方向が定められた最小とは限らない境界直方体を与える：

大きい点集合に使うことができる：

より高次元に使うことができる：

"FastBall"は境界Ballを与える．測度値が最小とは限らない：

大きい点集合に使うことができる：

より高次元に使うことができる：

"FastEllipsoid"は境界Ellipsoidを与える．測度値が最小とは限らない：

大きい点集合に使うことができる：

より高次元に使うことができる：

オプション  (5)

WorkingPrecision  (5)

デフォルトで，WorkingPrecisionはMachinePrecisionである：

より低い作業精度を指定する：

より高い作業精度を指定する：

InfinityというWorkingPrecisionは境界領域を厳密計算で評価する：

出力の精度は入力の精度によって制限される：

SetPrecisionを使って入力精度を上げると出力精度も高くなる：

Rationalizeを使って厳密数を得る．これで厳密計算が可能になる：

アプリケーション  (4)

3Dグラフィックスオブジェクトについて，さまざまな境界領域を求める：

境界領域を計算する：

体積をラベルとし，オブジェクトを境界領域とともに示す：

任意の領域の境界領域を求める：

DiscretizeRegionを使って領域を離散化する：

境界領域を計算する：

棄却サンプリングを使って任意の領域内のランダムな点を計算する：

ランダムな点が簡単に生成できる境界領域を求める：

境界領域内でランダムな点を生成する：

もとの領域に属する点を選ぶ：

結果を可視化する：

RandomPointを使ってもとの領域から生成された点と比較する：

境界領域は，境界領域間の衝突をオブジェクト同士の衝突よりもより簡単により速くチェックできるので，ゲーム物理でしばしば使われる：

オブジェクトの離散化近似を計算する：

境界領域が交差しないことをチェックすることでオブジェクトが衝突しないことを示す：

FindInstanceを使って境界領域が交差しないことをチェックする：

直接衝突をテストする方が時間がかかる：

しかし，たとえオブジェクトが衝突しなくても，境界領域は互いに素ではないかもしれない：

結果を可視化する：

特性と関係  (9)

点はすべて境界領域のメンバーである：

点のいくつかが境界領域の境界上にあることが多い：

"MinOrientedCuboid"は"MinCuboid"以下の体積を与える：

"MinOrientedRectangle"は，"MinRectangle"以下の面積を与える：

"MinConvexPolygon"は他の境界領域以下の面積を持つ：

"MinConvexPolyhedron"は他の境界領域以下の体積を持つ：

"MinConvexPolygon"は2DのConvexHullMeshに対応する：

"MinConvexPolyhedron"は3DのConvexHullMeshに対応する：

アフィン独立の3点の"MinConvexPolygon"はTriangleに対応する：

アフィン独立の4点の"MinConvexPolyhedron"はTetrahedronに対応する：

Circumsphereは2Dの3点を通る円を与える．対応する円板が境界領域である：

外接球のAreaは常に最小円板の面積以上である：

考えられる問題  (1)

BoundingRegionは要求された領域の退化した形を与えることがある：

Wolfram Research (2016), BoundingRegion, Wolfram言語関数， https://reference.wolfram.com/language/ref/BoundingRegion.html （2020年に更新）.

テキスト

Wolfram Research (2016), BoundingRegion, Wolfram言語関数， https://reference.wolfram.com/language/ref/BoundingRegion.html （2020年に更新）.

CMS

Wolfram Language. 2016. "BoundingRegion." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/BoundingRegion.html.

APA

Wolfram Language. (2016). BoundingRegion. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BoundingRegion.html

BibTeX

@misc{reference.wolfram_2024_boundingregion, author="Wolfram Research", title="{BoundingRegion}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/BoundingRegion.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_boundingregion, organization={Wolfram Research}, title={BoundingRegion}, year={2020}, url={https://reference.wolfram.com/language/ref/BoundingRegion.html}, note=[Accessed: 22-November-2024 ]}