BoundingRegion[{pt1,pt2,…}]
gives the minimal axis-aligned bounding box for the points pt1, pt2, ….
BoundingRegion[{pt1,pt2,…},form]
gives a bounding region of type form.
BoundingRegion[reg,form]
gives a bounding region for the region reg.


BoundingRegion
BoundingRegion[{pt1,pt2,…}]
gives the minimal axis-aligned bounding box for the points pt1, pt2, ….
BoundingRegion[{pt1,pt2,…},form]
gives a bounding region of type form.
BoundingRegion[reg,form]
gives a bounding region for the region reg.
Details and Options




- BoundingRegion is also known as enclosing region or circumscribed region.
- A bounding region
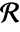 for a set of points
for a set of points 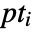 is a region such that
is a region such that 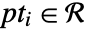 .
. - Optimal bounding regions typically minimize some property for the bounding region, such as the minimum area oriented rectangle. They generally take longer to compute.
- Fast bounding regions typically provide a bounding region quickly for a large number of points but may not provide the optimal bounding region, such as the minimum area oriented rectangle.
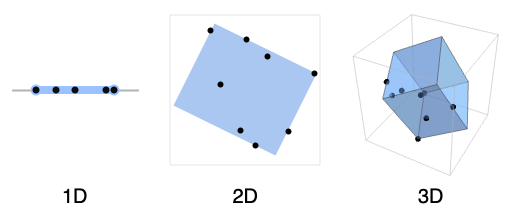
- Possible form specifications in 1D:
-
"MinInterval" min length interval - Possible form specifications in 2D:
-

"MinRectangle" min area axis-aligned rectangle 
"MinOrientedRectangle" min area oriented rectangle 
"MinConvexPolygon" min area convex polygon 
"MinDisk" min area disk 
"MinEllipse" min area ellipse 
"FastOrientedRectangle" fast bounding oriented rectangle 
"FastDisk" fast bounding disk 
"FastEllipse" fast bounding ellipse 
"FastStadium" fast bounding stadium - Possible form specifications in 3D:
-

"MinCuboid" min volume axis-aligned cuboid 
"MinOrientedCuboid" min volume oriented cuboid 
"MinConvexPolyhedron" min volume convex polyhedron 
"MinBall" min volume ball 
"MinEllipsoid" min volume ellipsoid 
"FastOrientedCuboid" fast oriented cuboid 
"FastBall" fast ball 
"FastEllipsoid" fast ellipsoid 
"FastCylinder" fast cylinder 
"FastCapsule" fast capsule - Possible form specifications in nD:
-

"MinCuboid" min measure axis-aligned cuboid 
"MinBall" min measure ball 
"MinEllipsoid" min measure ellipsoid 
"FastOrientedCuboid" fast oriented cuboid 
"FastBall" fast ball 
"FastEllipsoid" fast ellipsoid - BoundingRegion[reg] is equivalent to BoundingRegion[reg,"MinCuboid"].
- The following option can be given:
-
PerformanceGoal $PerformanceGoal aspects of performance to try to optimize WorkingPrecision MachinePrecision precision to use in computations
Examples
open all close allBasic Examples (4)
Scope (28)
1D (3)
2D (9)
"MinRectangle" gives the minimal area axis-aligned Rectangle:
Works for large collections of points:
"MinOrientedRectangle" gives the minimal area rectangle, not necessarily axis aligned:
Works for large collections of points:
"MinConvexPolygon" gives the minimal area polygon that contains the points:
Works for large collections of points:
"MinDisk" gives the minimal area Disk that contains the points:
Works for large collections of points:
"FastOrientedRectangle" gives an oriented bounding rectangle, which may not have the minimal area possible:
Works for large collections of points:
"FastDisk" gives a bounding Disk, which may not have the minimal area possible:
Works for large collections of points:
"FastEllipse" gives a bounding Ellipsoid, which may not have the minimal area possible:
Works for large collections of points:
"FastStadium" gives a bounding StadiumShape, not necessarily with the minimal area:
3D (11)
"MinCuboid" gives the minimal volume axis-aligned Cuboid:
Works for large collections of points:
"MinOrientedCuboid" gives the minimal volume cuboid, not necessarily axis aligned:
Works for large collections of points:
"MinConvexPolyhedron" gives the minimal volume polyhedron that contains the points:
Works for large collections of points:
"MinBall" gives the minimal volume Ball that contains the points:
Works for large collections of points:
"FastOrientedCuboid" gives an oriented bounding cuboid, not necessarily minimal:
Works for large collections of points:
"FastBall" gives a bounding Ball, which may not have the minimal volume possible:
Works for large collections of points:
"FastEllipsoid" gives a bounding Ellipsoid, not necessarily with the minimal volume:
Works for large collections of points:
"FastCylinder" gives a bounding Cylinder, not necessarily with the minimal volume:
Works for large collections of points:
"FastCapsule" gives a bounding CapsuleShape, not necessarily with the minimal volume:
Works for large collections of points:
 D (5)
D (5)
"MinCuboid" gives the minimal measure axis-aligned Cuboid:
Works for large collections of points:
"MinBall" gives the minimal measure Ball that contains the points:
Works for large collections of points:
Works with exact coefficients:
"FastOrientedCuboid" gives an oriented bounding cuboid, not necessarily minimal:
Works for large collections of points:
"FastBall" gives a bounding Ball, not necessarily with the minimal measure:
Works for large collections of points:
"FastEllipsoid" gives a bounding Ellipsoid, not necessarily with the minimal measure:
Options (5)
WorkingPrecision (5)
By default, the WorkingPrecision is MachinePrecision:
Specify lower working precision:
Specify higher working precision:
A WorkingPrecision of Infinity will evaluate a bounding region with exact calculations:
The precision of the output is limited by the precision of the input:
Use SetPrecision to increase the precision of the input, allowing for a higher-output precision:
Use Rationalize to get exact numbers. This allows for exact calculations:
Applications (4)
Find different bounding regions for a 3D graphics object:
Showcase the object with its bounding regions, using the volume as label:
Find bounding regions for an arbitrary region:
Use DiscretizeRegion to discretize the region:
Compute random points in an arbitrary region by rejection sampling:
Find a bounding region for which random points are easy to generate:
Generate random points in the bounding region:
Select the points that belong to the original region:
Compare with points generated from the original region using RandomPoint:
Bounding regions are often used in game physics because it is simpler and faster to check for collisions between bounding regions than between the objects themselves:
Compute discretized approximations of the objects:
Show that the objects do not collide by checking that their bounding regions do not intersect:
Use FindInstance to check that the bounding regions do not intersect:
Testing for collision directly takes more time:
However, even if the objects do not collide, bounding regions may not be disjoint:
Properties & Relations (9)
All points are members of their bounding region:
Typically, several points will be on the boundary of the bounding region:
"MinOrientedCuboid" gives smaller or equal volume than "MinCuboid":
"MinOrientedRectangle" gives smaller or equal area than "MinRectangle":
"MinConvexPolygon" will have smaller or equal area than other bounding regions:
"MinConvexPolyhedron" will have smaller or equal volume than other bounding regions:
"MinConvexPolygon" corresponds to ConvexHullMesh in 2D:
"MinConvexPolyhedron" corresponds to ConvexHullMesh in 3D:
"MinConvexPolygon" of three affinely independent points corresponds to Triangle:
"MinConvexPolyhedron" of four affinely independent points corresponds to Tetrahedron:
Circumsphere gives a circle through three points in 2D. The corresponding disk is a bounding region:
The Area for circumsphere is always greater than or equal to the area of the minimum disk:
Possible Issues (1)
Related Guides
Text
Wolfram Research (2016), BoundingRegion, Wolfram Language function, https://reference.wolfram.com/language/ref/BoundingRegion.html (updated 2020).
CMS
Wolfram Language. 2016. "BoundingRegion." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/BoundingRegion.html.
APA
Wolfram Language. (2016). BoundingRegion. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BoundingRegion.html
BibTeX
@misc{reference.wolfram_2025_boundingregion, author="Wolfram Research", title="{BoundingRegion}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/BoundingRegion.html}", note=[Accessed: 28-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_boundingregion, organization={Wolfram Research}, title={BoundingRegion}, year={2020}, url={https://reference.wolfram.com/language/ref/BoundingRegion.html}, note=[Accessed: 28-January-2026]}